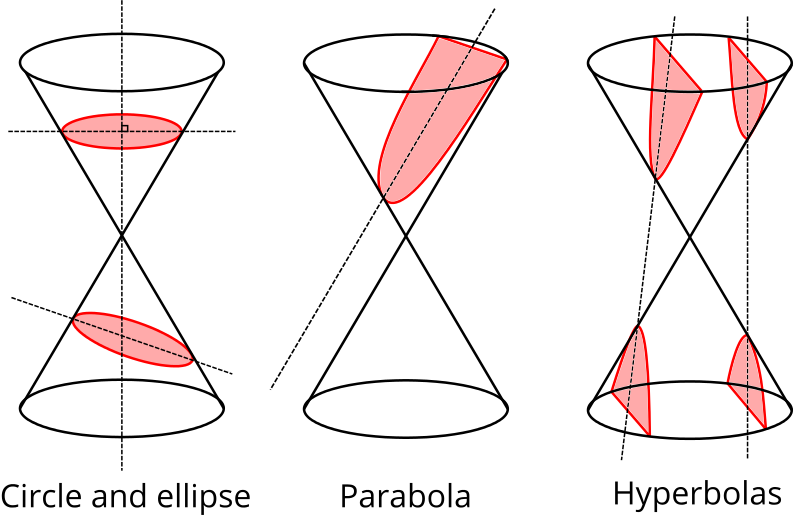
Euclid and Archimedes are just two of the ancient Greek mathematicians to have studied conic sections—the shapes created by slicing through a double cone with a flat plane. If the plane is perpendicular to the axis of the double cone, the intersection is a circle, and if the plane is angled parallel to the side of the cone the intersection is a parabola. If the plane cuts through both cones the intersection is a hyperbola. The only remaining case gives an ellipse.
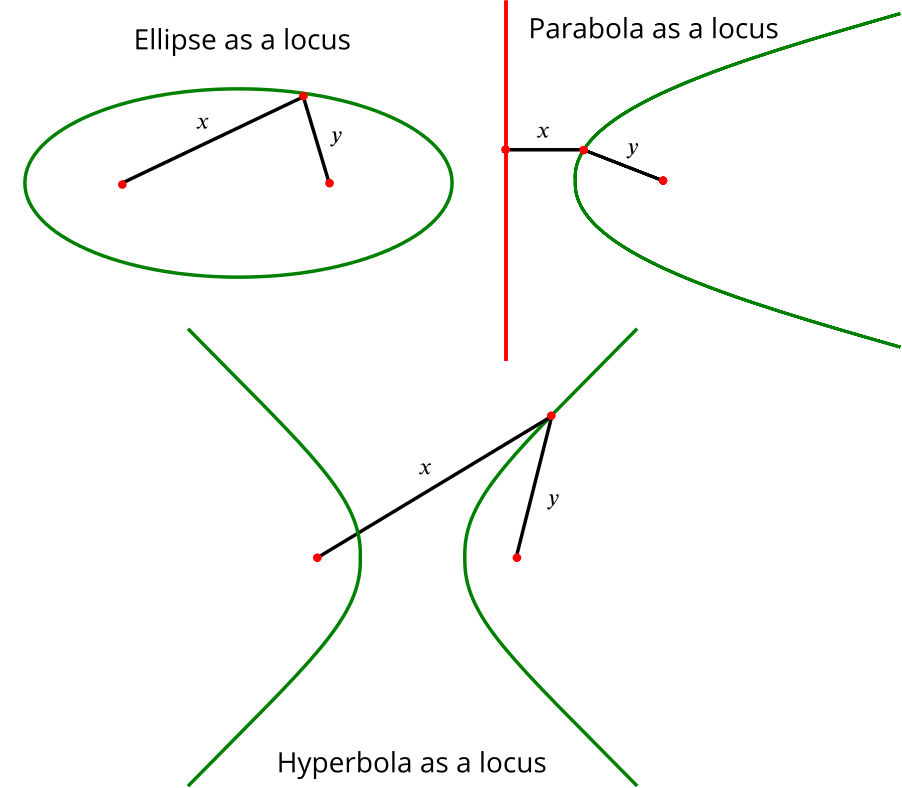
As well as having a description in terms of slicing through a cone, these shapes also have a description in terms of loci (locations) of points. A circle is the locus of points that are the same distance from the centre (the focus of the circle). An ellipse is the locus of points whose distances from two foci sum to a constant \(c\) (that is, \(x+y = c\) in the image below). A hyperbola is the locus of points that have the same difference \(c\) between distances from two foci (that is, \(|x-y| = c\)). A parabola is the locus of points equidistant from a focus and a straight line called the directrix (that is, \(x=y\)).
Skip forward a couple of millennia and the mathematical properties of the conic sections have a very modern application. Suppose that you are lost in the jungle, but that luckily you are equipped with a device that can transmit and receive information, a clock, and a map. Your device picks up a signal from my device, which tells you my exact location and the exact time I sent my signal.
Assuming you know how fast the signal travels, how can you use the information you have to determine how far away you are from me?
Suppose you have worked out that you are at distance \(d\) from me. Which conic section describes all your possible locations?
Suppose you have picked up two signals, one from me and one from another friend, Anna, telling you where on your map each of us is and at what time we sent the signal. How does that narrow down your possible locations?
Many smartphones are now able to use information sent out by GPS satellites (of which there are about nine overhead at any one time) in a similar way. Since the satellites are moving around in space, and therefore can’t be located on a two-dimensional map of the Earth, we now need to consider three-dimensional geometry. Can you work out how many satellites are needed to be sure of the location of a smartphone?
This method for finding a target’s location is called trilateration. Now let’s explore another method, multireceiver radar, which uses another conic section but requires fewer transmissions.
Suppose again that you are lost in the jungle but that this time you have no map. My friend Anna and I need to pinpoint your location to come and rescue you. I send you a signal, you immediately reply and Anna picks up the reply. Anna and I can communicate to establish the time that passed between me sending the signal and Anna receiving your reply.
What distance can Anna and I work out using that information?
Which conic section describes all your possible locations?
How many more people are needed to pinpoint your exact location? How many transmissions are needed?
One downside of this method is that it assumes the target will immediately reply to any signal we send. What if we can’t guarantee they will respond? Perhaps they don’t want to be found? Another conic section provides the answer.
Suppose now that you are hiding out in the jungle and that you are transmitting signals to your conspirators elsewhere. So as to not give away your location too easily your signals do not include information as to when they were sent. Anna and I can both pick up a signal sent by you and communicate to each other the time at which we received it. This means that we can work out the difference between the time it took the signal to reach me and the time it took to reach Anna.
What distance can Anna and I work out using that information?
Which conic section describes all your possible locations?
To pinpoint your exact location I need more colleagues, in addition to Anna, who can also pick up your signal and communicate with me. How many more colleagues do I need?
This covert technique, called multilateration, was used in WWI to locate enemy artillery ranges by listening to the sound of their gunfire. Mathematical ideas that are over 2,000 years old are used to find lost souls and uncover hidden enemies!
Further Reading
This material is based on content first published on Plus, the free online maths magazine:

