Here’s an interesting thought. If we’re told that \(122381 = 3 \times 35889 + 14714\) and that \(7\) divides both \(35889\) and \(14714\), then we know immediately that \(7\) also divides \(122381\).
Why is that? Try to find your own explanation.
We can use this idea to understand Euclid’s algorithm. You may have already explored Euclid’s algorithm in the Picture this! investigation.
Let’s run the algorithm on the numbers \(126\) and \(49\). We start by dividing \(126\) by \(49\), to find the quotient (in this case \(2\)) and the remainder (in this case \(28\)). We then repeat the process for the numbers \(49\) and \(28\), and so on. Here’s the list of equations that we get. \[\begin{align*} 126 &= 2 \times 49 + 28 \\ 49 &= 1 \times 28 + 21 \\ 28 &= 1 \times 21 + 7 \\ 21 &= 3 \times 7 \end{align*}\]We stop there because the remainder in the final equation is \(0\).
Here’s a handy tip. Numbers that do the same job are written in the same column. For example, the quotients are all just before the \(\times\) sign, and the remainders are all at the end. There’s a lot of flexibility about the order in which we write the components of these equations, but it’s a lot easier to keep track of which numbers are doing which jobs if we keep them in the same place each time.
What can we deduce from these equations?
The last non-zero remainder is \(7\), so we’d like to show that the highest common factor of \(126\) and \(49\) is \(7\). If you worked on Picture this!, then you might have been able to predict this: the relevant diagram is
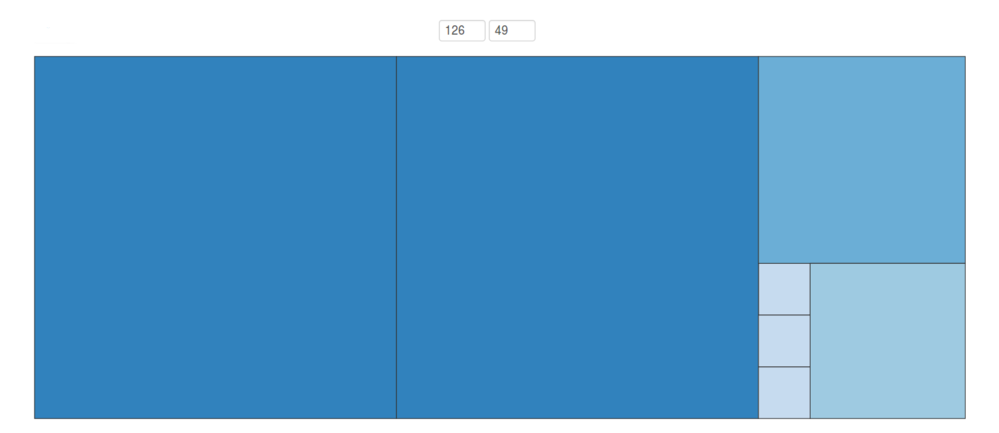
To show that \(7\) is the highest common factor of these two numbers, we need to show two things:
that \(7\) really is a common factor of them (it divides both numbers);
and that it’s the highest such number (any common factor of \(126\) and \(49\) is less than or equal to \(7\)).
We’ll show these things in turn.
\(7\) is a common factor of \(126\) and \(49\)
Of course, we could simply divide each number by \(7\) and check that we get an integer, but in fact we don’t need to do any more calculations: the equations above contain all the information we need. Let’s see how.
Let’s first start at the bottom and then work up.
The last equation, \(21 = 3 \times 7\), tells us that \(7\) divides \(21\).
The next equation up, \(28 = 1 \times 21 + 7\), then tells us that \(7\) divides \(28\) (because it divides both \(21\) and \(7\) on the right-hand side).
The next equation up, \(49 = 1 \times 28 + 21\), then tells us that \(7\) divides \(49\) (because it divides both \(28\) and \(21\) on the right-hand side).
Finally, the top equation, \(126 = 2 \times 49 + 28\) tells us that \(7\) divides \(126\) (because it divides both \(49\) and \(28\)). In particular, \(7\) is a common factor of \(126\) and \(49\).
You might reasonably think that it would be a lot easier just to check directly that \(7\) divides both numbers, but the advantage of what we’ve just done is that we can generalise it to any pair of starting numbers and still know that the last non-zero remainder divides both starting numbers.
Any common factor of \(126\) and \(49\) is less than or equal to \(7\)
Now let’s suppose that we have any old common factor of \(126\) and \(49\). Let’s call it \(d\).
It’s much easier to talk about something if we’ve given it a name, and \(d\) is a good name for a divisor.
Then the top equation, which we can rewrite as \(28 = 126 - 2 \times 49\), tells us that \(d\) divides \(28\) (because it divides both \(126\) and \(49\)).
The next equation down, which we can rewrite as \(21 = 49 - 1 \times 28\), tells us that \(d\) divides \(21\) (because it divides both \(49\) and \(28\)).
Finally, we can rewrite the penultimate equation as \(7 = 28 - 1 \times 21\). This tells us that \(d\) divides \(7\) (because it divides both \(28\) and \(21\)).
So if \(d\) is any common factor of \(126\) and \(49\), then it divides \(7\), and so is less than or equal to \(7\).
Conclusion
We have shown that any common factor of \(126\) and \(49\) is at most \(7\), and also \(7\) is a common factor of \(126\) and \(49\). But that means precisely that \(7\) is the highest common factor of \(126\) and \(49\).
We do not have to write out all of that explanation every time we use Euclid’s algorithm. But it’s important that we’re able to explain why the algorithm finds the highest common factor.
Pick your own pair of positive integers, and run Euclid’s algorithm on them. Now explain to a friend why your equations have found the highest common factor for you.
Here are some follow-up questions to help you develop your understanding of Euclid’s algorithm.
Find a pair of integers that have highest common factor \(12\) and where it takes exactly four steps of Euclid’s algorithm to find that highest common factor.
Can you still do this if you change the highest common factor and/or the number of steps?
Find a pair of four-digit numbers for which it takes very few steps for Euclid’s algorithm to find their highest common factor.
Find a pair of four-digit numbers for which it takes many steps for Euclid’s algorithm to find their highest common factor.

