A straight line to which a given curve eventually gets as close as we like, and stays close, is called an asymptote to the curve.
For example:
For the graph of \(y=\frac{1}{x}\), the \(x\)-axis and \(y\)-axis are both asymptotes: the curve gets as close as we like to the \(x\)-axis as \(x\) tends towards \(\infty\) or \(-\infty\), and as close to the \(y\)-axis as we like as \(x\) tends to zero.
For the graph of \(y=\ln(x)\) (where \(x>0\)), the \(y\)-axis is an asymptote: the curve gets as close as we like to it as \(x\) tends towards zero.
For the graph of \(y=2\), the line \(y=2\) is an asymptote: the curve \(y=2\) (actually a straight line) is as close as we like to itself as \(x\) tends towards \(\infty\).
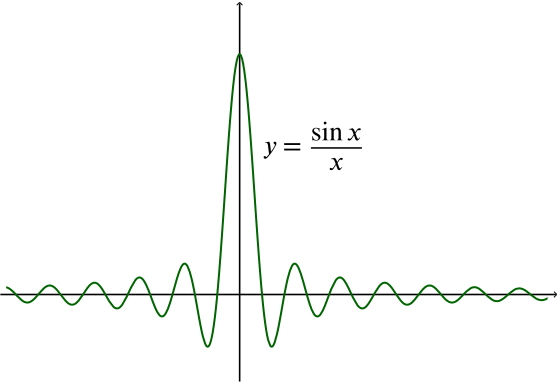
For the graph of \(y=\dfrac{\sin x}{x}\), the \(x\)-axis is an asymptote: as \(x\) tends towards \(\infty\) or \(-\infty\), even though the graph crosses the \(x\)-axis infinitely often, the curve gets as close as we like to the \(x\)-axis and stays close.