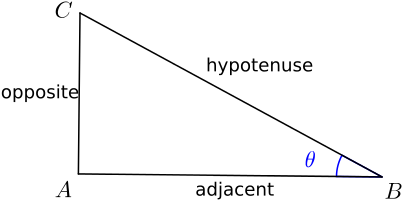
In a right-angled triangle, if one of the angles is \(\theta\), then the cosine of \(\theta\) is the length of the side adjacent to \(\theta\), divided by the length of the hypotenuse. That is, \[\cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}}.\]
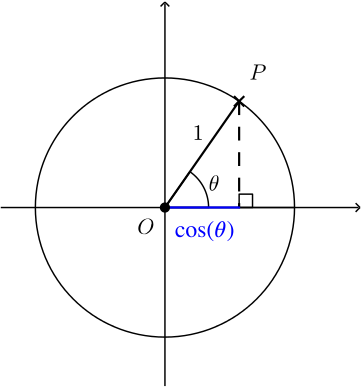
Alternatively, and more generally, \(\cos \theta\) is the \(x\)-coordinate of a point \(P\) obtained by rotating the point \((1,0)\) anti-clockwise about the origin through the angle \(\theta\).