Imagine driving round a bend in the road at a constant speed: the sharper the bend, the greater the acceleration. Curvature, \(\kappa\), is a measure of how sharply the curve bends: when the speed is \(v\), the acceleration is \(\kappa v^2\). (Throughout this glossary entry, we assume that we are working in a two-dimensional horizontal plane.)
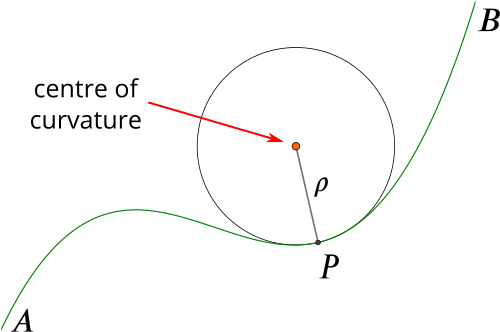
If we approximate the bend at this point by a circle (called the osculating circle), then the radius \(\rho\) of this circle is called the radius of curvature. The radius of curvature is related to the curvature by \(\kappa=1/\rho\). Thus the acceleration of the car can also be written as \(v^2/\rho\). This is the same as the formula for acceleration when travelling around an exact circle of radius \(r\), namely \(v^2/r\).
The definition of the curvature of a curve is \(\kappa =\dfrac{d\theta}{ds}\), where \(\theta\) is the angle the curve makes with a fixed direction at a point a distance \(s\) along the curve: in other words, it measures the rate of change of the direction of the curve as one moves along it at unit speed.
This also implies that if the curve is bending to the left (according to someone travelling along the curve), the curvature will be positive, while if it is bending to the right, the curvature will be negative. In the above example, the curvature of the curve at \(P\) is positive when traversing the curve from \(A\) to \(B\), but negative if traversing the curve in the opposite direction.
If the equation of the curve is given in parametric coordinates by \((x(t), y(t))\), then the curvature is given by: \[\kappa(t) = \frac{\dot{x} \ddot{y} - \ddot{x} \dot{y} } { ( \dot{x} ^2 + \dot{y} ^2 ) ^{3/2}},\] where the dot indicates the derivative with respect to \(t\).
If the curve is given by the formula \(y=f(x)\), then the equation for curvature becomes \[\kappa(x) = \frac{y''} { ( 1 + (y') ^2 ) ^{3/2}},\] where \(y'=f'(x)\) and \(y''=f''(x)\).

