An ellipse is a shape that is made by stretching a circle. It can also be obtained by making a slanting cut through a cone, and is therefore a type of conic section.
Shapes that look like an ellipse are said to be elliptical.
It is also (approximately) the path of an object that orbits the Sun or a planet.
The Cartesian equation of an ellipse centred on the origin with its axes (lines of symmetry) along the coordinate axes is \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.\] It can also be described parametrically as \[\begin{align*} x(t) &= a\cos t, \\ y(t) &= b\sin t. \end{align*}\]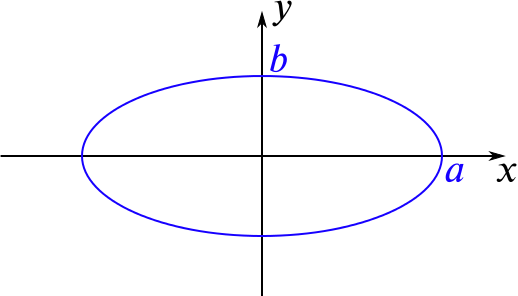
The longest and shortest lines through the centre of the ellipse are called the major axis and minor axis of the ellipse; in this case, these lie along the \(x\)-axis and \(y\)-axis. The lengths \(a\) and \(b\) are called the semi-major axis and semi-minor axis of the ellipse.

