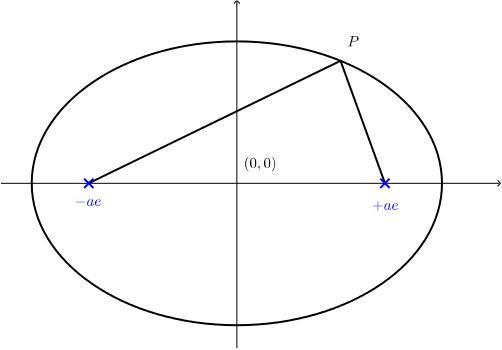
If \(A\) and \(B\) are two points, then the locus of points \(P\) such that \(AP + BP = c\) for a constant \(c>2 AB\) is an ellipse. \(A\) and \(B\) are the foci (plural of focus) of this ellipse.
If an ellipse has centre \((0,0)\), eccentricity \(e\) and semi-major axis \(a\) in the \(x\)-direction, then its foci are at \((\pm ae, 0)\) and its directrices are \(x=\pm a/e\).