The shape of graphs such as \(y = 1/x\) or \(y^2 - x^2 = 1\) is a hyperbola. It is a type of conic section.
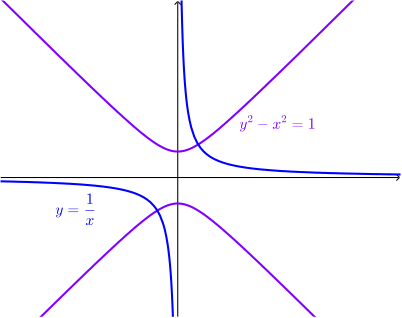
It is also (approximately) the path of an object that falls into the solar system, is flung out again by the Sun’s gravity, and never returns.
The Cartesian equation of a hyperbola centred on the origin with its axes (lines of symmetry) along the coordinate axes and crossing the \(x\)-axis is \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1.\] One of the branches can also be described parametrically as \[\begin{align*} x(t) &= a\cosh t, \\ y(t) &= b\sinh t \end{align*}\] or both branches can be described as \[\begin{align*} x(t) &= a\sec t, \\ y(t) &= b\tan t. \end{align*}\]
