A function is called periodic if it repeats itself over and over again at regular intervals.
Formally, a function \(f\) is periodic with period \(T\) (where \(T>0\)) if \(f(x+T)=f(x)\) for all \(x\). The smallest such positive \(T\) is called the least period (or often just “the period”) of the function. (If \(f\) is a constant function, then it is periodic with every possible period, but it doesn’t have a “least period”.)
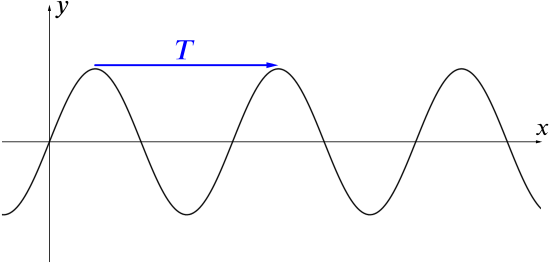
For example, \(\sin x\), \(\cos x\) and \(\tan x\) are all periodic. For \(\sin x\) and \(\cos x\), the (least) period is \(2\pi\), while for \(\tan x\), the (least) period is \(\pi\).

