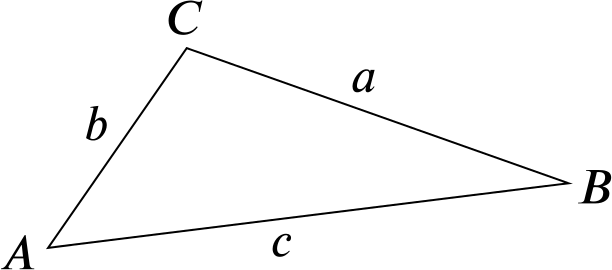
The sine rule states that if \(a\), \(b\) and \(c\) are the lengths of the sides of a triangle, and \(A\), \(B\) and \(C\) are the angles in the triangle; with \(A\) opposite \(a\), etc., then \[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}.\] This ratio is also equal to \(2R\), where \(R\) is the radius of the circumcircle of \(ABC\). Some regard this further equality as part of the sine rule.
Another name sometimes used for the sine rule is the law of sines.