|
|
 |
|
Written by Martin Hyland, co-director of Underground Mathematics
In the last newsletter we proudly introduced our new website. Naturally we shall be further developing the site and we wish to promote it and the philosophy which underlies it. We hope for support from readers of our newsletter.
In this newsletter I would like to give a glimpse of some of the work we are doing. Our tubemap makes it clear that Geometry is important in providing connections. But geometry and visualisation can also support specific understanding. Consider the trigonometric functions. Their basic properties come from the fact that cosine and sine parameterize the unit circle; and - as the old-fashioned terminology circular functions suggests - it helps to see them in terms of circular motion. (From this point of view it is bizarre that circular motion has been lurking in the M3 Module at A level.)
An example may help in seeing the kinds of issues involved. Suppose we ask students to determine for which A and B we have sin A = sin B and for which we have cos A = cos B. How might students see things? Consider some possibilities.
1. They could at a stretch use trig identities and algebraic manipulation. If they succeed then hats off to them (and their teachers).
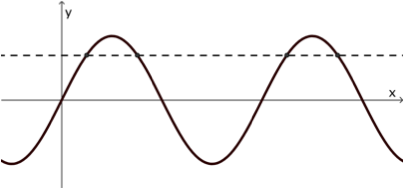
2. They could sketch the graphs of sin and cos, and try to work it out by looking at intersections with horizontal straight lines. That requires a cool head but surely the visualisation helps.

3. They could look at a circle at the origin and draw chords parallel to the two axes. With a sense of circular motion and a little imagination one can immediately write down the answer.
There are other ways one could envisage approaching the problem but there is something quite compelling about 3. The only problem with it - I suppose - is that it requires a good deal of mathematical insight and understanding. But after all that is exactly what we hope to elicit in students. The challenge for us is to create resources which support that endeavour in the classroom.
I would like to close by stressing that we are keen to have feedback on the website, the resources on it and indeed on everything which we are doing.
Best wishes,
Martin Hyland
|
|
In the spotlight: Underground Mathematics philosophy
|
|
|
In each newsletter we focus on an area of Underground Mathematics. This time we are looking at the philosophy behind the project.

In the about section on the website we describe our approach and the beliefs that inform our work. Alongside this is a 5 minute video that shows the team, teachers and students discussing our resources being used in the classroom.
We encourage you to watch this video – perhaps as part of a departmental meeting, and we offer a few questions that might be the starting point for a discussion: - What mathematical behaviours do students exhibit in the video?
- Do you recognise any of these from your own experience?
- What opportunities or challenges do you think using Underground Mathematics resources might present in your school?
|
|
Clare Hill, from Twynam School, shares her experience of using Which is bigger?, an ideal resource for a new year 12 group in September.
The resource ‘Which is bigger’ has proved to be a particularly powerful activity to work on early in year 12. It reveals a great deal about the students’ thinking and their perceptions of what a graph actually represents.
I have often found that students start their A Level courses saying that they don't like graphs but this activity opens a useful conversation about how graphs can give us an immediate response to a problem in a simple, diagrammatic way.
This activity also reveals students’ misconceptions regarding the dependence and independence of variables and many arrive at sixth form without understanding that when we talk about a graph being ‘positive’ or ‘negative’ we are actually referring to the y values - because they are the dependent values. This concept becomes extremely important for students when they are working on quadratic inequalities and may be an argument for introducing this activity in year 11 for the new GCSE.
The power of a good sketch is also reinforced through this activity and in the pictures below, the students came to the conclusion that an accurately drawn graph from a table of values yielded no more information than a quick (but accurate) sketch. This was a skill we were able to refer back to through the remainder of the course, helping students to conceptualise the problem in hand.
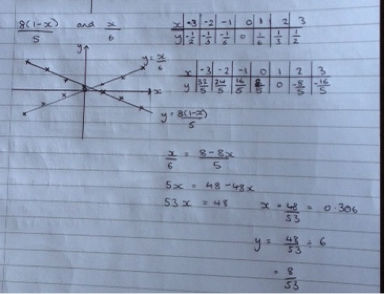
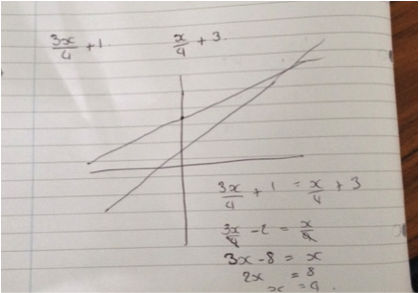
|
|
Underground Mathematics Community
|
|
|
The Underground Mathematics site is accessible to all, and its design is rooted in teacher experience. So we would value any contribution you can make by sharing your experiences of using our resources with your students. You can join the conversation by creating a login for the site and using the ‘Discuss’ link that appears at the top of each page.
Our Twitter feed is @UndergroundMath, where we regularly tweet resource suggestions, events we are involved in and any interesting maths we come across. This replaces @CMEPMaths. You can also find Underground Mathematics on Facebook here.
|
|
Over the next few months you can find the team at the following conferences.
Maths Teachers’ Conference, Belfast, 9th June
British Society for Research into Learning Mathematics, Loughborough University, 10th-11th June
MEI Conference, University of Bath, 30th June – 2nd July
NW Maths Hubs Conference, Manchester Metropolitan University, 5th July
NQT inspiration day, Cambridge, 12th July
International Congress on Mathematical Education, Hamburg, 24th – 30th July
East Midlands KS5 Maths Conference, Nottingham, 9th August
|
Centre for Mathematical Sciences
University of Cambridge
Wilberforce Road
Cambridge
CB3 0WB
01223 766857
info@undergroundmathematics.org
https://undergroundmathematics.org
|
|

