Between any two whole numbers there is a fraction. Between \(0\) and \(1\) there is \(\frac{1}{2}\), between \(1\) and \(2\) there is \(1 \frac{1}{2} = 3/2\), and so on. In fact, there are infinitely many fractions between any two whole numbers. Let’s see why.
Between \(0\) and \(1\) there are also \(\frac{1}{3}\), \(\frac{1}{4}\), \(\frac{1}{5}\), and any number that can be written as \(\frac{1}{n}\) where \(n\) is some whole number. In addition there are fractions like \(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{4}{5}\), and so on. More generally, if \(m\) and \(n\) are positive whole numbers and \(m\) is smaller than \(n\), then \(\frac{m}{n}\) is a fraction that lies between \(0\) and \(1\). In a similar way, there are also infinitely many fractions in between any other pair of whole numbers.
Numbers that can be written as fractions are called rational numbers. These include the whole numbers, since a whole number can be written as a fraction with \(1\) in the denominator: \(1=\frac{1}{1}\), \(2=\frac{2}{1}\), and so on. And as we have just seen, there are not only infinitely many rational numbers in the whole number line, but there are also infinitely many rational numbers in just the small interval between two consecutive whole numbers.
But we can go even further than this. If you give me any two rational numbers \(x\) and \(y\) on the number line, then no matter how close together they are, I can always find infinitely many other rational numbers that lie between them.
One way of doing this is as follows. Imagine all the numbers as lying along a ruler. Suppose you have given me \(x = \frac{1}{100}\) and \(y= \frac{2}{100}\). The two are very close together, the difference \(d\) is \[d = y-x =\frac{2}{100} - \frac{1}{100} = \frac{1}{100}.\] The difference \(d\) is the length of the little interval that lies between \(x\) and \(y\) on the ruler.
Now suppose I chop that little interval between \(x\) and \(y\) in half. The number \(z\) that corresponds to the midpoint obviously lies between \(x\) and \(y\). The distance from \(x\) to that number \(z\) is \(\frac{1}{100} \times \frac{1}{2} = \frac{1}{200}\). So the number \(z\) is \[z = x+\frac{1}{200} = \frac{1}{100}+\frac{1}{200} = \frac{3}{200}.\]
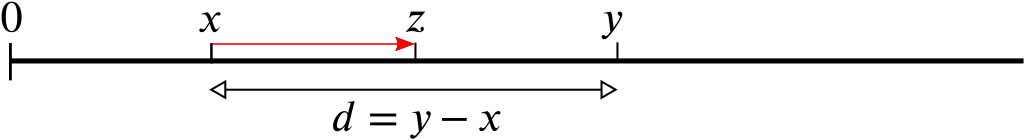
It is also a rational number, since it can be written as a fraction. Any sum or product of two rational numbers is always itself a rational number, since when you add or multiply two fractions you always get another fraction.
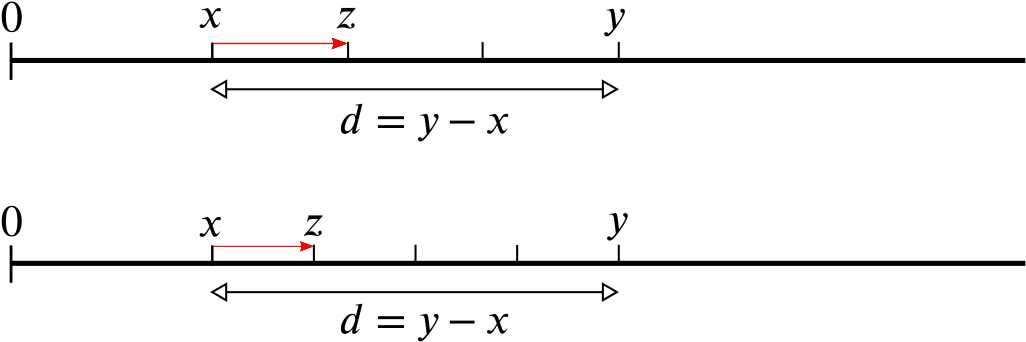
So I have just found you a rational number \(z\) that lies in between \(x\) and \(y\). But I could find infinitely many others in the same way. Rather than chopping the distance in half, I could have chopped it in three, four, five, a hundred, or any number \(n\) of pieces, giving me \(n\) little intervals. The distance from \(x\) to the right endpoint \(z\) of the first interval is then \(\frac{1}{100} \times \frac{1}{n}\). The point \(z\) itself is \[z = x+\frac{1}{n} = \frac{1}{100}+\frac{1}{n}.\]
It’s a rational number, since (as we noted above) products and sums of rational numbers are themselves rational numbers.
Since this works for any positive whole number \(n\), and there are infinitely many of those, I have just managed to find infinitely many rational numbers that lie between \(x\) and \(y\). The same kind of argument works for any two rational numbers \(x\) and \(y\), not just our two specific examples. Therefore, whatever two rational numbers \(x\) and \(y\) you pick on the number line, I can always find infinitely many other rational numbers that lie between them. Fractions really are everywhere.

