Everybody always wants to make the best of things: get there the fastest, get the biggest serve or spend the least money. And all of these problems, and many other types of problems in maths and physics, are down to maximising or minimising something – finding which conditions give you the biggest or smallest answer to the question you are asking.
For certain problems, this is just a matter of looking at, or mathematically analysing a graph. For example, if you want to know the maximum height a ball reaches when thrown in the air, you could look at a graph of height versus time:
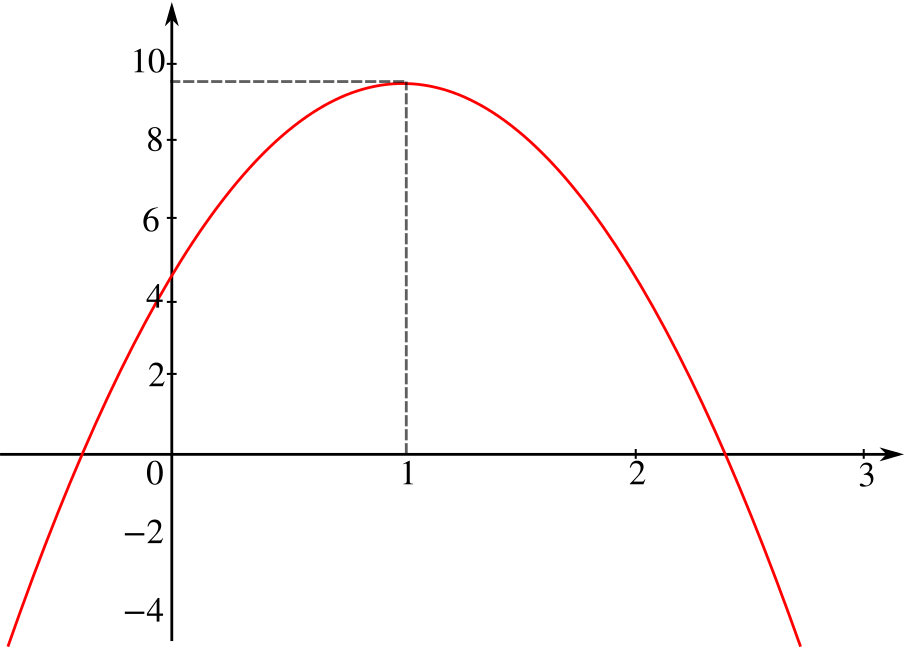
A ball is thrown from the top of a double decker bus (approximately \(\quantity{4.5}{m}\) tall) with an initial upward velocity of \(\quantity{10}{m\,s^{-1}}\). The height of the ball is given by the equation \(h = -5t^2 + 10t + 4.5\).
- Draw a height-time graph for the motion of the ball.
- What is the maximum height of the ball?
This approach works if the quantity you want to maximise or minimise depends on one variable, but it also works when the quantity depends on more variables. If this is the case then you can describe the quantity you are interested in by a function and identify the maximum or minimum of this function either graphically or using calculus (as we saw in Why gradients are important in mathematics).
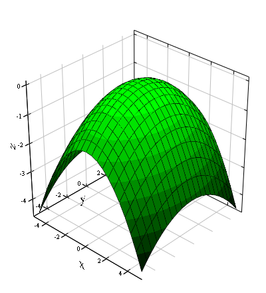
A function is defined as \(f(x,y) = x^2 + y^2 -2x + y\).
Using GeoGebra, or other graphing software, find the minimum value of the function.
But what if the quantity you are interested in depends on a function itself? For example, what if you wanted to find the path of a ball that minimised the time the ball took to travel from one point to another? This quantity depends on the shape of the path, which is a function rather than a variable. To find the maxima or minima in this situation we need something which is a sort of generalisation of calculus: a method called calculus of variations.
Calculus of variations was first developed when, in 1696, Johann Bernoulli (one of the famously mathematical Bernoulli family from Switzerland) asked the great mathematical minds of the day to solve something called the brachistochrone problem. Picture a bead falling (under the force of gravity) along a frictionless wire pegged to a vertical plank of wood – what shape should the wire take so that the bead’s fall from the top to the bottom of the wire takes the least amount of time?
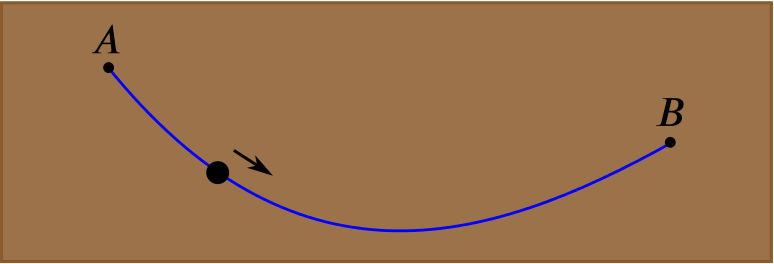
To solve this problem it was necessary to consider all the possible curves the wire could take. Some of the great names of the age – including Isaac Newton, Gottfried Liebniz, Guillaume de l’Hopital, and Johann Bernoulli and his brother Jakob – all came up with the solution: the quickest path is a cycloid – the path traced out by a point on a circle as it rolls along a straight line.
\[ \text{(Video courtesy of Zorgit)} \]
Solving this problem was where the calculus of variations began, and it continued to develop over the following centuries thanks to many great mathematicians such as Euler and Lagrange in the 18th century, Gauss, Cauchy and Weierstrass in the 19th century, and Hilbert and Noether in the 20th century. It is still an important mathematical tool today for problems that involve optimisation.
Calculus of variations also solves some very old problems, such as Queen Dido’s problem from 800BC, where she was trying to find the shape that would contain the maximum possible area . It is also one of the ways to derive the shape of a hanging chain, called a catenary.