Imagine a ray of light being reflected by a mirror. The law of reflection says that the angle between the incoming ray and the mirror is equal to the angle between the reflected ray and the mirror.
To see what exactly this means, let’s think about this set-up in two dimensions – it’s alright to do this since the incoming ray and the reflected ray determine a plane, and in order to understand how the reflection works we only need to consider that plane. The mirror is now represented by a straight line segment, and so are the incoming and reflected rays of light. Let’s write \(P\) for the point at which the ray meets the mirror. See the image below. The angle \(\alpha\) is called the angle of incidence and the angle \(\beta\) is called the angle of reflection. The law of reflection says that \(\alpha=\beta.\)
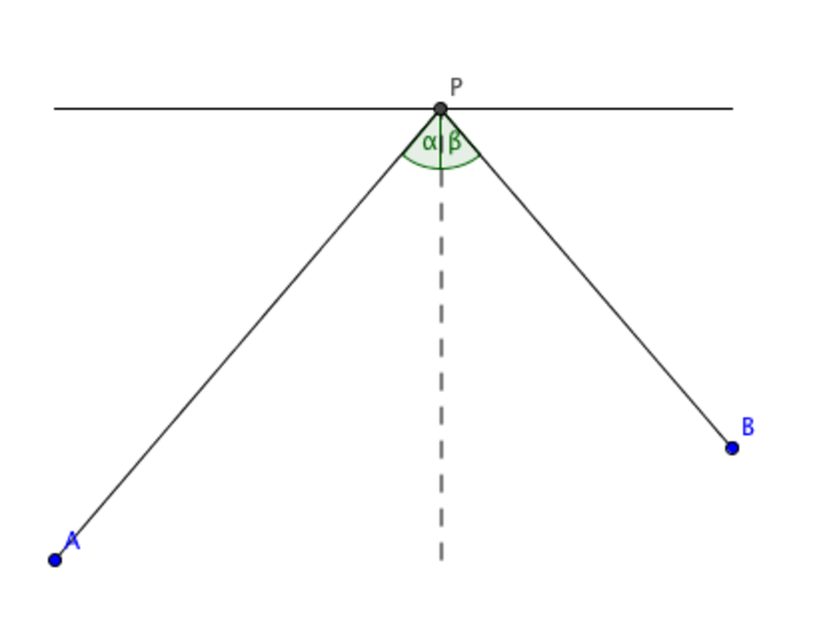
Note that \(\alpha\) and \(\beta\) are the angles between the ray segments and the line that is perpendicular to the mirror, which is called the normal at \(P\). This is just a convention. We could equally well have phrased the law in terms of the angles at which the rays meet the mirror, as these are just \(90-\alpha\) and \(90 - \beta\) respectively.
How do we know that light always behaves in this way when it is being reflected? We can actually prove that it does if we assume that light always takes the path of shortest distance (via the mirror) when travelling between two points. (It’s a reasonable assumption: when you shine a torch at night, the beam will always be a straight line as long as there is no obstacle to reflect or refract it in the way.) Let’s write \(A\) for the point at which the incoming light ray starts and \(B\) for the point at which we observe the reflected ray.
By playing with the animation below convince yourself that the distance from \(A\) to \(B\) via the point \(P\) (since we are reflecting) is shortest when the angles \(\alpha\) and \(\beta\) are equal. Move the slider to vary the position of \(P\) and thereby the size of the angles.
Since light travels at constant speed (it doesn’t speed up or slow down), assuming that it travels along the path of shortest distance (via the mirror) is equivalent to assuming it travels along the path that takes the shortest time. This idea is known as Fermat’s principle, after the 17th century mathematician Pierre de Fermat (although others had come up with the principle before him). It’s an example of a principle of least action: the assumption that, when faced with a choice, nature always chooses the option that involves the least effort. For another method of approaching this optimisation problem, see Calculus of variations.
We can derive the law of reflection from Fermat’s principle mathematically, using a little calculus. In the diagram below we have written \(d\) for the horizontal distance between \(A\) and \(B\) and \(x\) for the horizontal distance between \(A\) and the normal. The horizontal distance between \(B\) and the normal is therefore \(d-x\). The vertical distances from \(A\) and \(B\) to the mirror are \(a\) and \(b\) respectively.
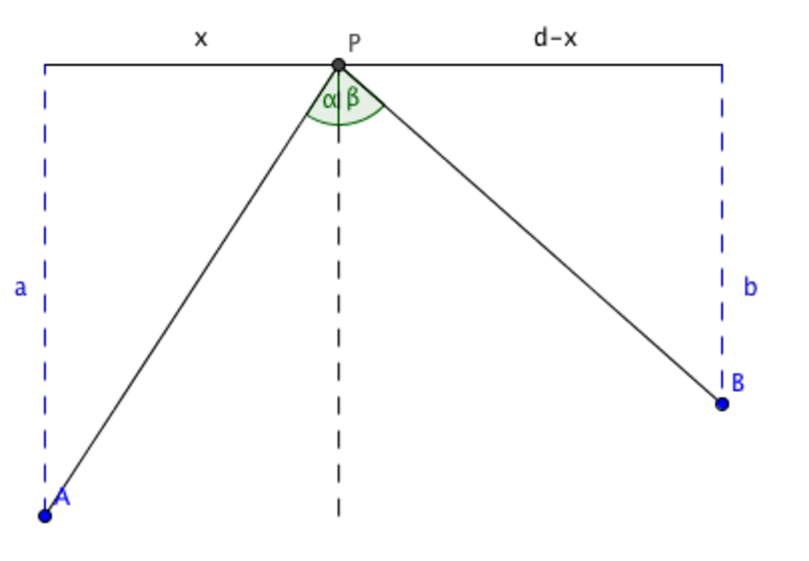
What is the distance \(AP\)?
What is the distance \(BP\)?
What is the total distance travelled by the ray?
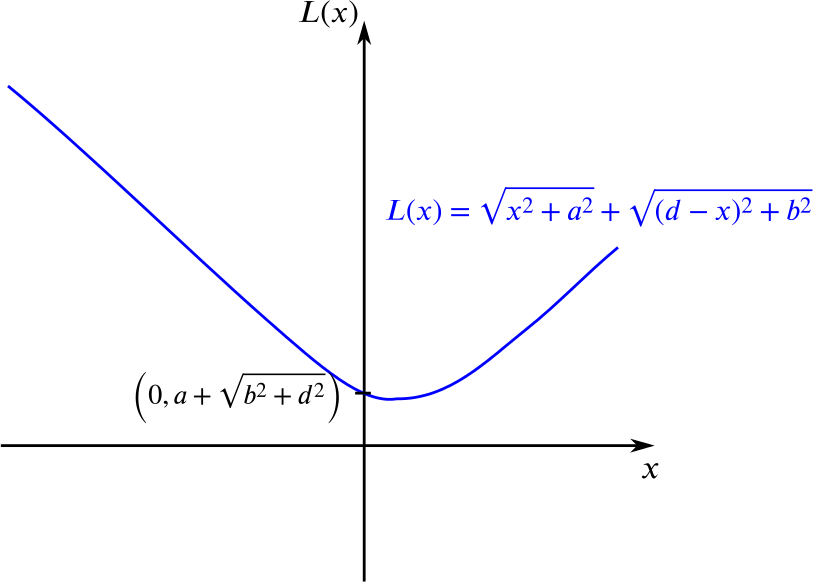
We write this distance as \(L(x)\) because it depends on the length \(x\), which in turn depends on the angle \(\alpha\).
What value of \(x\) minimises the function \(L(x)\) (makes it the shortest)?