In this question we shall consider the function \(f(x)\) defined by \[f(x) = x^2 - 2px + 3\] where \(p\) is a constant.
- Show that the function \(f(x)\) has one stationary value in the range \(0< x <1\) if \(0< p <1\), and no stationary values in that range otherwise.
We know that \(y = f(x)\) is a parabola, and since the coefficient of \(x^2\) is positive, it is ‘vertex-down’ and has a minimum. It can only have one stationary value.
Differentiating \(f(x)\) gives \[f'(x) = 2x - 2p,\] so the stationary point occurs when \(x=p\), which is in the range \(0<x<1\) if and only if \(0<p<1\).
Or else completing the square, \(f(x) = (x-p)^2 + 3 - p^2\), and so the vertex of the parabola is at \((p, 3-p^2)\), which is in the range \(0<x<1\) if and only if \(0<p<1\).
In the remainder of the question we shall be interested in the smallest value attained by \(f(x)\) in the range \(0 \le x \le 1\). Of course, this value, which we shall call \(m\), will depend on \(p\).
- Show that if \(p \ge 1\) then \(m=4-2p\).
The minimum value \(m(p)\) attained by \(f(x)\) in the range \(0 \le x \le 1\) will occur either at an endpoint (\(x=0\) or \(x=1\)), or at a stationary point in between 0 and 1.
If \(p \ge 1\) then we have seen there is no stationary point in that interval. So as \(f(1)=4-2p<3=f(0)\), we have \(m(p)=4-2p\).
- What is the value of \(m\) if \(p \le 0\)?
For \(p \le 0\), again, no stationary point exists in the range \(0 \le x \le 1\). We now have \(f(0) = 3 < 4 - 2p = f(1)\), so \(m(p)=3\).
- Obtain a formula for \(m\) in terms of \(p\), valid for \(0 < p < 1\).
If \(0 < p < 1\), then we know there is a stationary point of \(f\) at \(x=p\), which is at the parabola’s vertex.
So the minimum value \(m(p)=f(p)=3-p^2.\)
- Using the axes opposite, sketch the graph of \(m\) as a function of \(p\) in the range \(-2 \le p \le 2\).
To summarise the results of parts ii), iii) and iv) the function \(m(p)\) is: \[m(p)= \begin{cases} 3 &\text{if } p \le 0 \\ 3-p^2 &\text{if } 0 < p < 1 \\ 4-2p &\text{if } 1 \le p \end{cases} \]
A sketch of this looks like
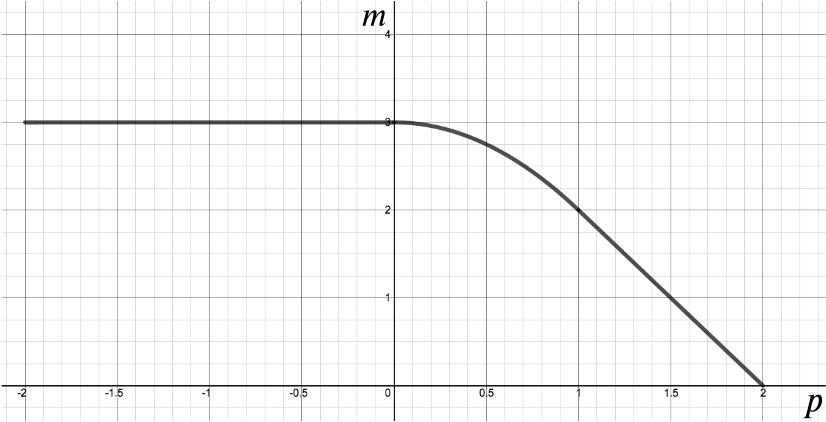
How do we know for sure that the join at \(p=1\) is smooth? Because the gradient of \(3-p^2\) is \(-2p\) and the gradient of \(4-2p\) is \(-2,\) which agree when \(p=1\).

