Can we find a curve from its gradient function?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The first part of the question tells us that \[ \frac{dy}{dx} = 4x - 3. \] so we know that \[\begin{equation}\label{eq:indefinite-eq-for-y} y = \int \frac{dy}{dx} \:dx = 2x^2 - 3x + c \end{equation}\]

for some constant \(c\). (This is a consequence of the fundamental theorem of calculus.)

The curve is a parabola and since the coefficient of \(x^2\) is positive we know its single stationary point is a minimum. We are also given that the \(y\)-value at the minimum is \(-\dfrac{1}{8}\).

This minimum occurs where \(\dfrac{dy}{dx} = 0 \implies x = \dfrac{3}{4}\). Substituting into equation \(\eqref{eq:indefinite-eq-for-y}\), we have that \[\begin{align*} -\frac{1}{8} = 2 \left( \frac{3}{4} \right)^2 - 3 \cdot \frac{3}{4} + c &\implies c = -\frac{1}{8} - \frac{9}{8} + \frac{9}{4} \\ &\implies c = 1. \end{align*}\]

So we know that the equation of the curve is \(y = 2x^2 - 3x + 1\).

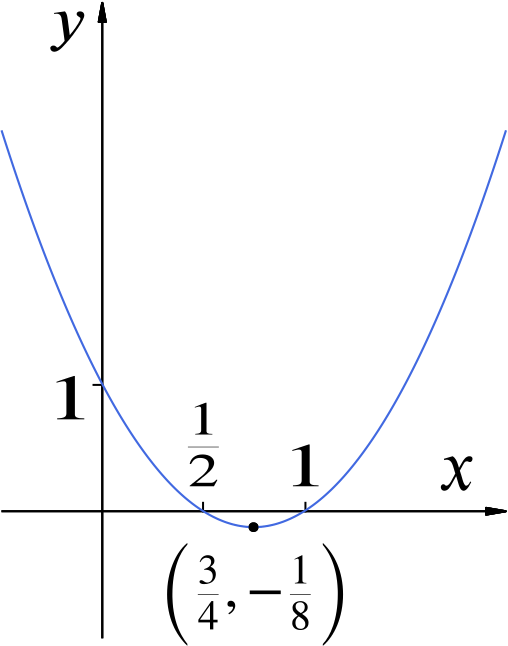
We can factorise the expression for \(y\) as \[ y = 2x^2 - 3x + 1 = (2x - 1)(x - 1). \] We thus have that the equation \(y = 0\) has two roots, at \(x = \dfrac{1}{2}\) and \(1\). The graph has a minimum at the point \(\left( \dfrac{3}{4}, -\dfrac{1}{8} \right)\), and finally, the \(y\)-intercept of the function is \(1\).