Let \[I(c)=\int_0^1 ((x-c)^2 +c^2)dx\] where \(c\) is a real number.
- Sketch \(y=(x-1)^2+1\) for the values \(-1\le x\le 3\) and show on your graph the area represented by the integral \(I(1)\).
We have \(y=(x-1)^2+1\) so since \((x-1)^2 \ge 0\), with equality if and only if \(x=1\), the minimum value of \(y\) is \(1\), which occurs when \(x=1\).
Rewriting as \(y=x^2-2x+2\), we see that the \(y\)-intercept is at \(y=2\). This gives us enough information to sketch the graph.
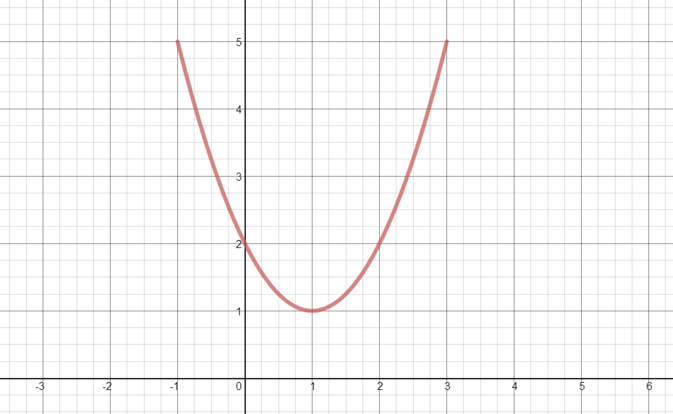
Here is the area represented by the integral.
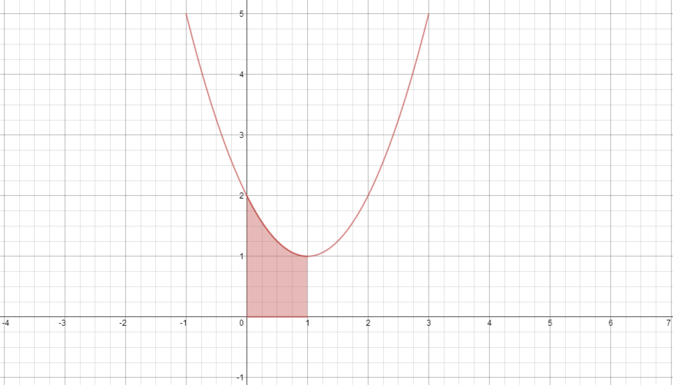
- Without explicitly calculating \(I(c)\), explain why \(I(c) \ge 0\) for any value of \(c\).
The integrand \((x-c)^2+c^2\) is greater than or equal to zero for any real \(c\) since \((x-c)^2\) and \(c^2\) are both squares of real numbers and so are both greater than or equal to zero. So we must have the integral of their sum greater than or equal to zero.
Or we could say that \(y=(x-c)^2+c^2\) is a parabola pointing downwards with vertex \((c, c^2)\), which is above the \(x\)-axis, and so the integral is positive.
- Calculate \(I(c)\).
- What is the minimum value of \(I(c)\) (as \(c\) varies)?
So the minimum value that \(I(c)\) can take is \(5/24\). (This occurs when \(c=1/4\).)
- What is the maximum value of \(I(\sin \theta)\) as \(\theta\) varies?
Note that from our work above, the MINIMUM value of \(I(\sin\theta)\) happens when \(\theta = \arcsin (0.25)\).
Now \(c=\sin \theta\) varies between between \(-1\) and \(1\), so we need to find the maximum value of \(I\) over this range.
We worked out earlier that the overall minimum of \(I\) occurs at \(c=1/4\), and since \(I\) is quadratic, it is symmetric about this point, and increasing for larger and smaller values of \(c\).
So the maximum value of \(I(c)\) over the range \(-1 \le c \le 1\) occurs at \(c=-1\), the furthest point from \(x=1/4\) in the range.
So the maximum value of \(I(\sin \theta)\) is \(I(-1)=10/3\).

