The function \(y\) is defined by \(y=3x-2x^2\). Write down its derivative and show that, when \(x=5\), a small increase in \(x\) of \(p\%\) causes an increase in the magnitude of \(y\) of approximately \(17p/7\%\).
The derivative of \(y=3x-2x^2\) is \(y'=\dfrac{dy}{dx}=3-4x\), so when \(x = 5, y = -35\) and \(y'=-17\).
We now approximate the curve with the tangent to the curve at \(x=5,\) which is justified if we are close to \((5,-35)\).
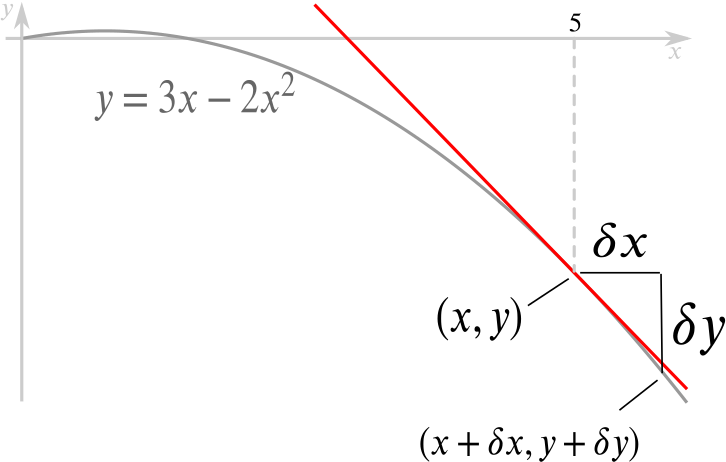
Suppose that \((x + \delta x, y + \delta y)\) is on the curve. Then we can express the percentage increase in \(x\) by \[ \frac{\delta x}{x}\times 100=p, \] and similarly the percentage increase in \(y\) by \[ \frac{\delta y}{y} \times 100 = q. \] Dividing these, we get \(\dfrac{\delta y}{\delta x} \dfrac{x}{y} = \dfrac{q}{p}\). Now if \(\delta x\) and \(\delta y\) are small, \(\dfrac{\delta y}{\delta x} \approx \dfrac{dy}{dx}\), so at \(x = 5, \dfrac{q}{p} \approx -17 \times \dfrac{5}{-35}\).
This gives us that \(q = \dfrac{17p}{7}\), and therefore the magnitude of \(y\) increases by approximately \(\dfrac{17p}{7}\) per cent.

