When is the area of a face of this pyramid a minimum?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

The volume \(V\) of a square based pyramid is \[V=\dfrac{1}{3}bh,\] where \(b\) is the area of the base and \(h\) is the height.

Where does this formula come from?

To see where this formula comes from (it holds for pyramids with any base, and cones too) consider a unit cube:

Now draw in the four diagonals from each of the pairs of opposite corners like this:

This makes six identical square based pyramids from each of the faces:

Each pyramid has a base of area one and is of height \(1/2\). Each one must also have a volume of \(1/6\), which is \(\dfrac{1}{3}bh\).

We can extend this for cubes of a different side length, and cuboids.

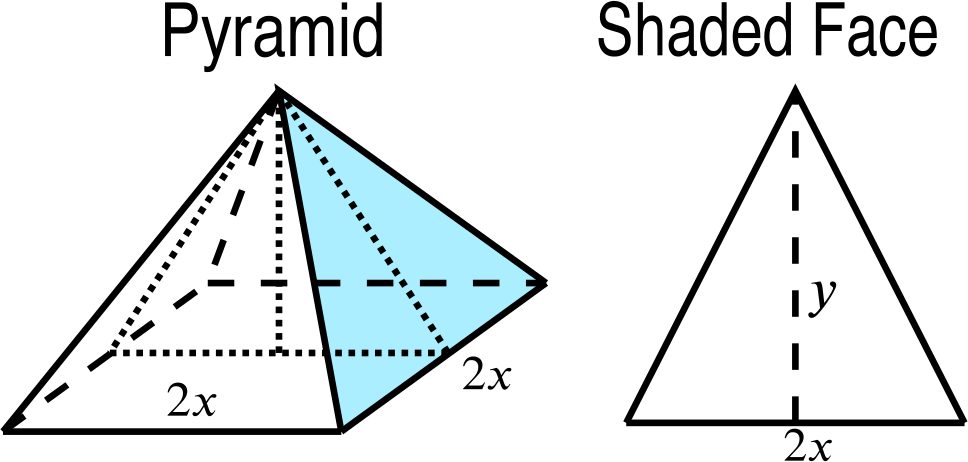
Our pyramid looks like this:

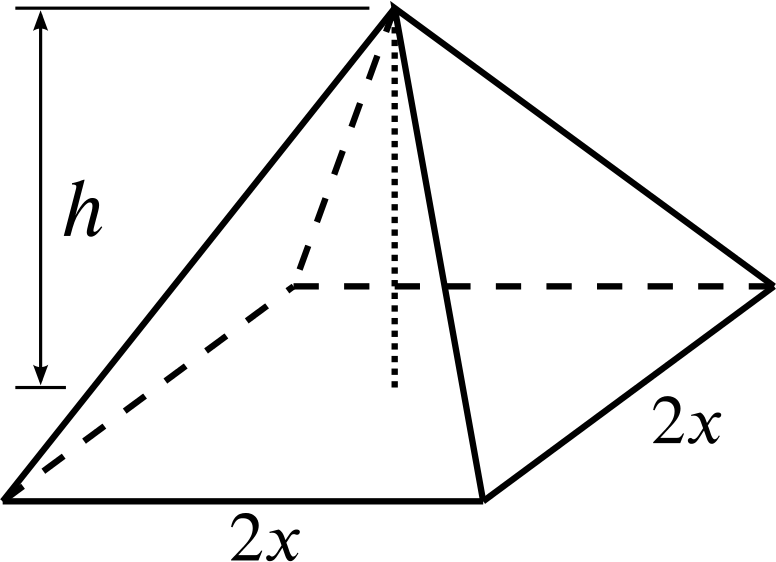
So we have \[V=\frac{1}{3}(2x)^2h.\]

We need to find the area of a sloping triangular face (which will be the same for all four faces, since the vertex is directly above the centre of the base).

For this, we need the height \(y\) of the face, which is related to \(h\) and \(x\) via \[y^2=h^2+x^2,\] which we can see from taking a vertical cross-section of the pyramid.

The area of the face is \(A=\frac{1}{2}(2x)y=xy\).

Therefore, \[A^2=x^2y^2=x^2(h^2+x^2)=x^2\left(\left(\frac{3V}{4x^2}\right)^2+x^2\right)=x^2\left(\frac{9V^2}{16x^4}+x^2\right)=\frac{9V^2}{16x^2}+x^4,\] as required.

We can say that \(A\) has a turning point if and only if \(A^2\) does, since we know \(A\) is positive and \(y=x^2\) is an increasing function for \(x > 0\).

So considering \[\frac{d(A^2)}{dx}=4x^3+\frac{9V}{16}\frac{-2}{x^3}=4x^3-\frac{9V^2}{8x^3},\] we find stationary points when \(\dfrac{d(A^2)}{dx}=0.\) \[\Longrightarrow \qquad 4x^3-\frac{9V^2}{8x^3}=0 \qquad \Longrightarrow \qquad 32x^6=9V^2.\] There will be two real roots of this equation, one negative (which doesn’t interest us) and one positive, so there is one stationary point in the \(x>0\) region.

We know \[\frac{d(A^2)}{dx}=\frac{32x^6 - 9V^2}{8x^3},\] so if \(x\) increases slightly from \(\left(\dfrac{9V^2}{32}\right)^\frac{1}{6}\), then \(x^6\) increases slightly from \(\dfrac{9V^2}{32}\), (since \(y = x^6\) is an increasing function for \(x > 0\)), which tells us that the gradient of \(y = A^2\) is positive. Similarly if \(x\) decreases slightly from \(\left(\dfrac{9V^2}{32}\right)^\frac{1}{6}\), the gradient is negative.

So our single stationary point for \(x > 0\) must be a local minimum, and we know that \(A^2\) (and hence \(A\)) is minimized when \(x^6=\dfrac{9V^2}{32}\).

Now \(h^2 = \dfrac{9V^2}{16x^4}=\dfrac{9V^2}{32x^6}2x^2\), and so if \(x^6 = \dfrac{9V^2}{32}\), then \(h^2 = 2x^2\), and \(y^2 = x^2 + h^2 = 3x^2\).

So \(y = \sqrt{3}x\), and each face must be an equilateral triangle.