The figure shows part of a curve passing through \(6\) points \(A,B,C,D,E,F\).
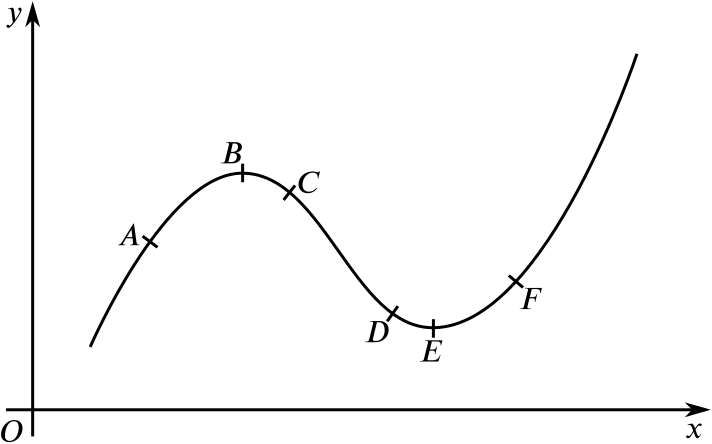
Copy and fill in the following table showing, for each of the points, whether
\(\dfrac{dy}{dx}\) is positive (\(+\)), negative (\(-\)), or zero (\(0\)),
\(\dfrac{dy}{dx}\) is increasing (\(I\)), or decreasing (\(D\)), as \(x\) increases.
The filled in table should look like this:
| \(A\) | \(B\) | \(C\) | \(D\) | \(E\) | \(F\) | |
|---|---|---|---|---|---|---|
| \(\dfrac{dy}{dx}\) is \(+,-,\) or \(0\) | \(+\) | \(0\) | \(-\) | \(-\) | \(0\) | \(+\) |
| \(\dfrac{dy}{dx}\) is \(I\) or \(D\) | \(D\) | \(D\) | \(D\) | \(I\) | \(I\) | \(I\) |
To see whether \(\dfrac{dy}{dx}\) is positive, negative or zero, we can imagine the tangent to the curve at each point and think about its gradient.
- If we imagine the tangent to the curve at a point and move the point along the curve from left to right, we can see that its gradient starts positive and decreases. At \(B\) it changes from positive to negative and is still decreasing. There is a point somewhere between \(C\) and \(D\) where the gradient stops decreasing and starts increasing.
We call this a point of inflection. It happens when the gradient function has a maximum or a minimum. We learn more about this at the next station.
Determine which of (a) and which of (b) apply at the point \(\left(3,3\tfrac{1}{3}\right)\) on the curve \(y=x+\dfrac{1}{x}\).
The derivative of \(y=x+\dfrac{1}{x}\) is \[\frac{dy}{dx}=1-\frac{1}{x^2} ,\] which is positive at \(x=3\).
There are many ways to find if \(\dfrac{dy}{dx}\) is increasing or decreasing, here are three ways you might determine it.
- Calculation. We could evaluate \(\dfrac{dy}{dx}\) at values of \(x\) above and below \(3\) and compare them:
\(x=\) \(2\) \(3\) \(4\) \(\dfrac{dy}{dx}=\) \(\dfrac{3}{4}\) \(\dfrac{8}{9}\) \(\dfrac{15}{16}\) We can see that the value of \(\dfrac{dy}{dx}\) increases as \(x\) increases.
Algebra. We could rewrite \(\dfrac{dy}{dx}=\dfrac{x^2-1}{x^2}\). This makes it clear that for \(x\geq 1\) \(\dfrac{dy}{dx}>0\) and as \(x\) gets larger \(\dfrac{dy}{dx}\) gets closer and closer to \(1\), so \(y\) is increasing at \(x=3\).
Graph sketching. A sketch of the graph \(y=1-\dfrac{1}{x^2}\) shows that \(y\) is increasing at \(x=3\). And therefore the gradient of \(y=x+\dfrac{1}{x}\) is increasing.
Can you find any other ways to determine if it is increasing or decreasing?

