The figure shows the curve \(y = x^2\) and the straight line \(2x + y = 15\). Find
- the co-ordinates of \(P\) and \(Q\),
The figure given in the question is the following.
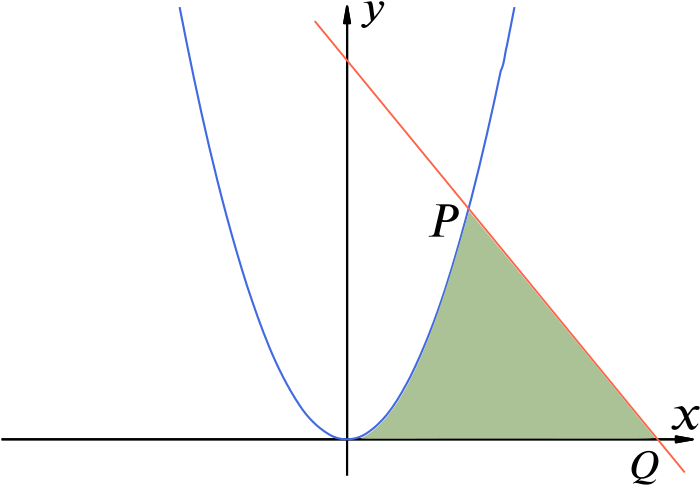
The point \(P\) is the point in the first quadrant at which the curve \(y = x^2\) and line \(y = 15 - 2x\) cross. That is, it is the point whose \(x\)-coordinate is positive and such that \[ x^2 = 15 - 2x. \] This equation can be rearranged to become \[ x^2 + 2x - 15 = 0 \] which, by inspection, factorises: \[ (x + 5)(x - 3) = 0. \] Thus, the \(x\)-coordinate of \(P\) is \(3\), and so the coordinates of \(P\) are \((3,9)\) since, in particular, \(P\) lies on the curve \(y = x^2\).
The point \(Q\) is the \(x\)-intercept of the line, so the \(x\)-coordinate of \(Q\) is the value of \(x\) such that \[ 15 - 2x = 0. \] Thus, \(x = \tfrac{15}{2}\), and so the coordinates of \(Q\) are \(\left( \tfrac{15}{2}, 0 \right)\).
- the area of the shaded region.
The key to this question is to break the region into two pieces, as the following diagram shows.
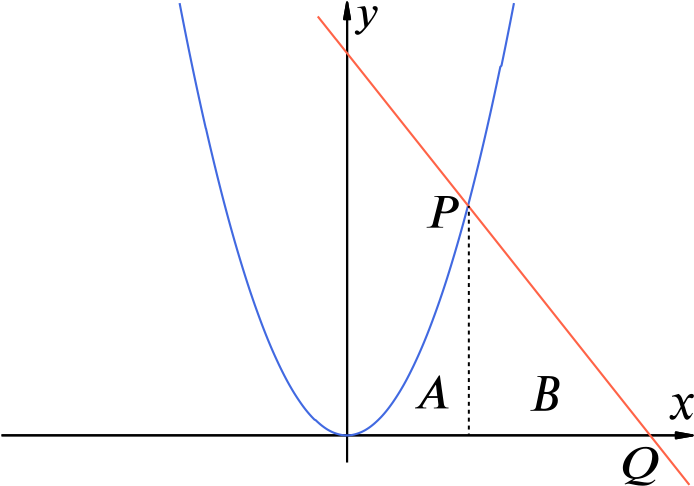
The shaded area is therefore the sum of the area of region \(A\) and the area of region \(B\), which are separated by the dotted line segment in the image. This dotted line segment is part of the line \(x = 3\), since the \(x\)-coordinate of the point \(P\) is \(3\).
The area of region \(A\) can be calculated by integration: \[ \text{area of $A$} = \int_0^3 x^2 \:dx = \left[ \frac{x^3}{3} \right]_0^3 = \frac{3^3}{3} - 0 = 9. \]
On the other hand, region \(B\) is a (right-angled) triangle whose base has length \[ \frac{15}{2} - 3 = \frac{9}{2} \] (which corresponds to the \(x\)-coordinate of \(P\) being subtracted from the \(x\)-coordinate of \(Q\)) and whose height has length \(9\), which corresponds to the \(y\)-coordinate of \(P\). Thus, \[ \text{area of $B$} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times \frac{9}{2} \times 9 = \frac{81}{4}. \]
Therefore, \[ \text{area of shaded region} = \text{area of $A$} + \text{area of $B$} = 9 + \frac{81}{4} = \frac{117}{4}. \]

