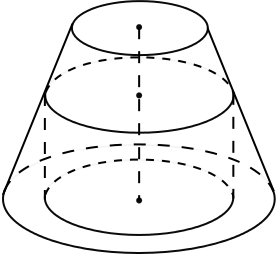
A truncated cone of height \(h\) has circular ends of radii \(2r\) and \(r\). In this cone is inserted a circular cyclinder having its axis along the axis of the cone. One end of the cylinder lies in that face of the cone which is of radius \(2r\) and the circumference of the other end lies in the curved surface of the cone (see diagram). Given that the radius of the base of the cylinder is \(s\), show that the volume of the cylinder is
\[\frac{\pi h s^2(2r - s)}{r}.\]
If \(s\) is allowed to vary, find, in terms of \(h\) and \(r\), the maximum volume of the cylinder.

