Show that the equation \[x^3+3x^2 - 3 = 0\] has one positive root.
Consider the equation \[y=x^3 +3x^2 - 3.\]
Approach 1
When \(x=0\), \(y=-3<0\), and when \(x=1\), \(y=1>0\), so since the curve is continuous (we can draw it without taking our pen off the paper), it must cut the \(x\)-axis somewhere betwwen \(x=0\) and \(x=1\).
Could it cut the positive \(x\)-axis more than once? Well, we can see that \(x^3\) and \(3x^2\) are increasing functions for positive \(x\).
If there were to be a second positive root, the curve would have to decrease somewhere for \(x > 0\), which is not possible.
So the curve has a single positive root.
Approach 2
Here we find the turning points of the curve.
Differentiating gives \[\frac{dy}{dx} = 3x^2 + 6x = 3x(x+2),\] and so setting \(\dfrac{dy}{dx}=0\) and solving gives \(x=0\) or \(x=-2\). Therefore, the turning points lie at \((0,-3)\) and \((-2,1)\).
It is now clear that \((-2,1)\) is a maximum and \((0,-3)\) is a minimum, as \(1>-3\).
We can now sketch the graph:
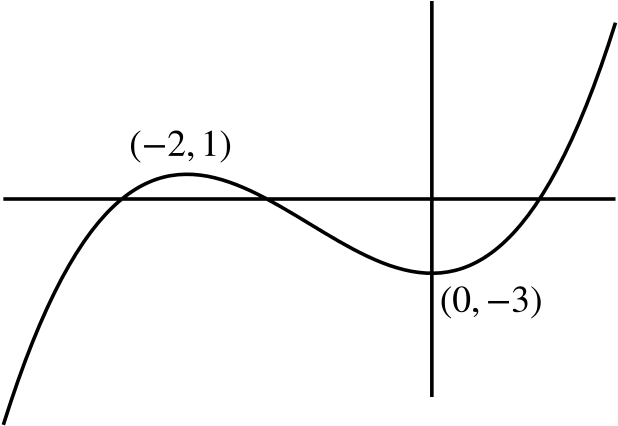
We can see that the equation has exactly one positive root.
Find to three decimal places an approximation to this root.
Method 1: Trial and improvement
We first find two integers that the root lies between, then use the same technique to find the root to one decimal place, and so on.
| \(x\) | \(0\) | \(1\) | \(0.5\) | \(0.8\) | \(0.9\) | \(0.85\) | \(0.86\) | \(0.87\) | \(0.88\) | \(0.875\) | \(0.876\) | \(0.877\) | \(0.878\) | \(0.879\) | \(0.8795\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(y\) | -\(3\) | \(1\) | -\(2.125\) | -\(0.568\) | \(0.159\) | -\(0.128\) | -\(0.145\) | -\(0.070\) | \(0.004\) | -\(0.033\) | -\(0.025\) | -\(0.018\) | -\(0.011\) | -\(0.003\) | \(0.001\) |
So \(x\) lies between \(0.879\) and \(0.8795\), so to three decimal places, \(x \approx 0.879\).
Method 2: Linear interpolation
We first find two integers that the root lies between, as in Method 1. Writing \(f(x)=x^3+3x^2-3\), we find that \(f(0)=-3\) and \(f(1)=1\).
This suggests that the root is much closer to \(1\) than to \(0\), and we can use linear interpolation to improve our estimates, as shown in this diagram:
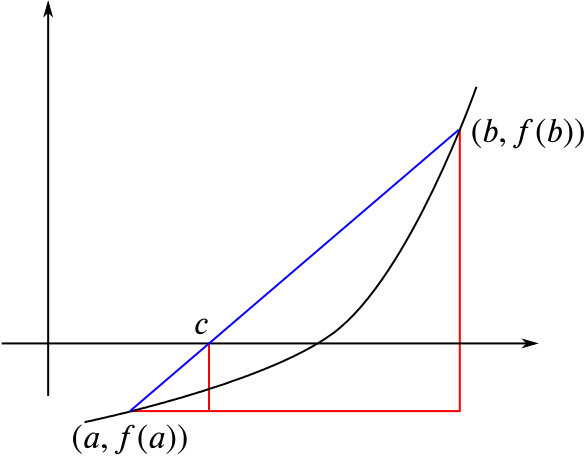
If our estimates are \(x=a\) and \(x=b\), giving \(f(a)<0\) and \(f(b)>0\), then our new estimate \(c\) is given by similar triangles (as explored in the resource In-betweens). We have \[\frac{c-a}{b-a}=\frac{0-f(a)}{f(b)-f(a)},\] so rearranging gives \[c=a-\frac{(b-a)f(a)}{f(b)-f(a)}.\]
If \(f(c)\) turns out to be negative (as in the example shown), then the root lies between \(c\) and \(b\), so we use \(c\) and \(b\) for the next iteration. If \(f(c)\) turns out to be positive, then the root lies between \(a\) and \(c\), so we use \(a\) and \(c\) for the next iteration.
| \(a\) | \(b\) | \(f(a)\) | \(f(b)\) | \(c\) | \(f(c)\) |
|---|---|---|---|---|---|
| \(0\) | \(1\) | \(-3\) | \(1\) | \(0.75\) | \(-0.89\) |
| \(0.75\) | \(1\) | \(-0.89\) | \(1\) | \(0.86777\) | \(-0.08748\) |
| \(0.86777\) | \(1\) | \(-0.08748\) | \(1\) | \(0.87841\) | \(-0.00743\) |
| \(0.87841\) | \(1\) | \(-0.00743\) | \(1\) | \(0.87930\) | \(-0.00062\) |
| \(0.87930\) | \(1\) | \(-0.00062\) | \(1\) | \(0.87938\) | \(-0.00005\) |
It looks as though we are almost there: to confirm this, we calculate \(f(0.8795)=0.00087>0\), so the root lies between \(0.87930\) and \(0.8795\), so is \(0.879\) to three decimal places.
Method 3: Newton-Raphson iteration
Here we start with an estimate for the root, say \(x=a\), and draw a tangent to the curve from here. Our next estimate is the intersection of the tangent with the \(x\)-axis.
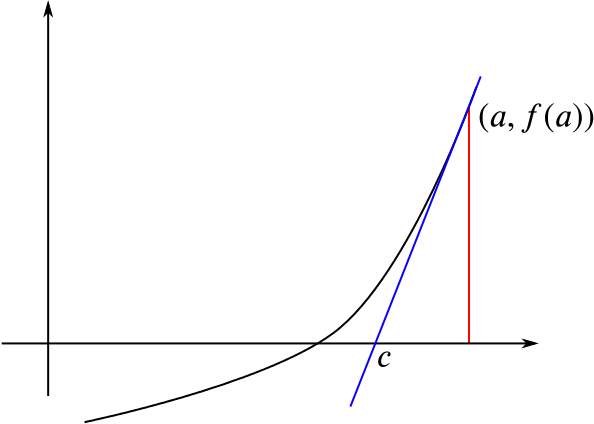
The tangent has gradient \(f'(a)\), so we see that \[\frac{f(a)}{a-c}=f'(a).\] Rearranging this to find \(c\) gives \[c=a-\frac{f(a)}{f'(a)}.\] Once we have found our \(c\), we use that as our next value of \(a\).
Since we therefore have an iteration here, we could write \(x_0\) for our initial value of \(a\), then \(x_1\) for the next, and so on, and our formula can be written as \[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\]
In our case, \(f'(x)=3x^2+6x\), so the formula is \[c=a-\frac{x^3+3x^2-3}{3x^2+6x}.\]
We cannot start with \(a=0\), as then the denominator would be \(0\) (what does this correspond to in terms of the graph?)
So we start with \(a=1\):
| \(a\) |
|---|
| \(1\) |
| \(0.888889\) |
| \(0.879452\) |
| \(0.879385\) |
(We can use the ANS button on our calculator to help us here). The last two values agree to three decimal places. So checking \(f(0.879)=-0.0029\) and \(f(0.8795)=0.00087\) (or using \(f(0.879452)=0.00051,\) which we’ve already had to calculate) shows that the root is \(0.879\) to three decimal places.
Which of these methods is the simplest, do you think?
Which requires the fewest calculations? (Especially remembering that there were no electronic pocket calculators in the 1950s!)
Are there other methods which might have been even better?

