Find the equation of the tangent to the rectangular hyperbola \(xy=c^2\) at the point \(P(ct,c/t)\).
Differentiating the curve \(y=\dfrac{c^2}{x}\) we find
\[\dfrac{dy}{dx}=-\dfrac{c^2}{x^2}.\]
So the gradient at \(P = (ct,c/t)\) is \(-\dfrac{1}{t^2}\).
Thus the equation of the tangent here is \[\begin{align*} y-\dfrac{c}{t} &= -\dfrac{1}{t^2}(x-ct) \\ \Longrightarrow y &= -\dfrac{x}{t^2}+\frac{2c}{t} = \dfrac{2ct-x}{t^2} \end{align*}\]- Prove that the area of the triangle \(MOL\) is \(2c^2\)
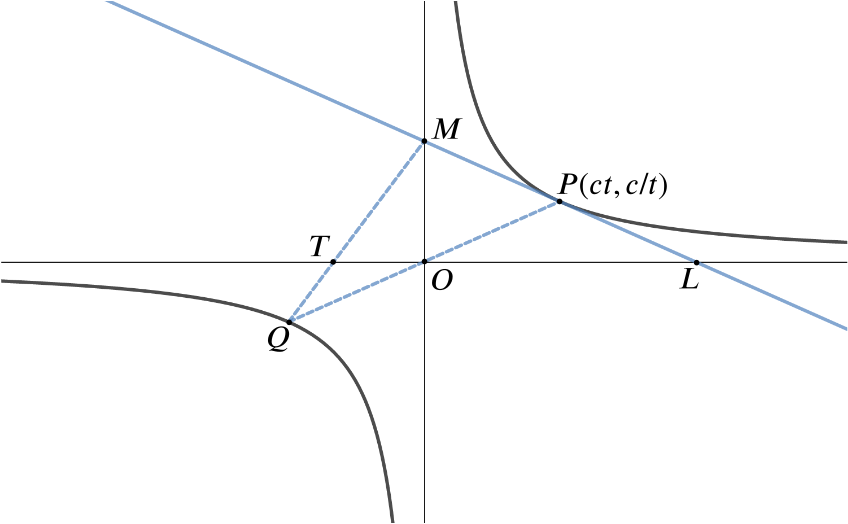
The \(x\)-intercept of the tangent: \[0=\dfrac{2ct-x}{t^2}\quad \Longrightarrow \quad x=2ct,\] so \(L\) is \((2ct,0)\).
The \(y\)-intercept of the tangent: \[y=\dfrac{2ct}{t^2}=\dfrac{2c}{t},\] so \(M\) is \((0,\dfrac{2c}{t}).\)
So using area = \(\dfrac{1}{2} \times \,\text{base}\, \times\, \text{height}\), the area of triangle \(MOL\) is \[\dfrac{1}{2}\times 2ct \times \dfrac{2c}{t}=2c^2.\]
- Prove that the area of the triangle \(QOT\) is \(c^2/3\).
The coordinates of point \(Q\) are \((-ct,-c/t)\) since it is the reflection of \(P\) in \(O\).
The line joining \(Q = (-ct,-c/t)\) and \(M = (0,2c/t)\) has gradient \[\dfrac{\dfrac{2c}{t}+\dfrac{c}{t}}{ct}=\dfrac{3}{t^2}.\] Therefore the equation of the line \(QM\) is \[y-\dfrac{2c}{t}={3}{t^2}x.\] The \(x\)-intercept is then \[x=-\dfrac{2c}{t}\times\dfrac{t^2}{3}=-\dfrac{2ct}{3}.\]
Thus triangle \(QOT\) has base \(\dfrac{2ct}{3}\) and height \(\dfrac{c}{t}\) so its area is \[\dfrac{1}{2}\times \dfrac{2ct}{3}\times\dfrac{c}{t}=\dfrac{c^2}{3}.\]

