Consider two functions \[f(x) = a - x^2,\] \[g(x) = x^4 - a.\]
For precisely which values of \(a > 0\) is the area of the region bounded by the \(x\)-axis and the curve \(y = f(x)\) bigger than the area of the region bounded by the \(x\)-axis and curve \(y = g(x)\)?
- all values of \(a\),
- \(a > 1\),
- \(a > \dfrac{6}{5}\),
- \(a > \left(\dfrac{4}{3}\right)^{3/2}\),
- \(a > \left(\dfrac{6}{5}\right)^4\).
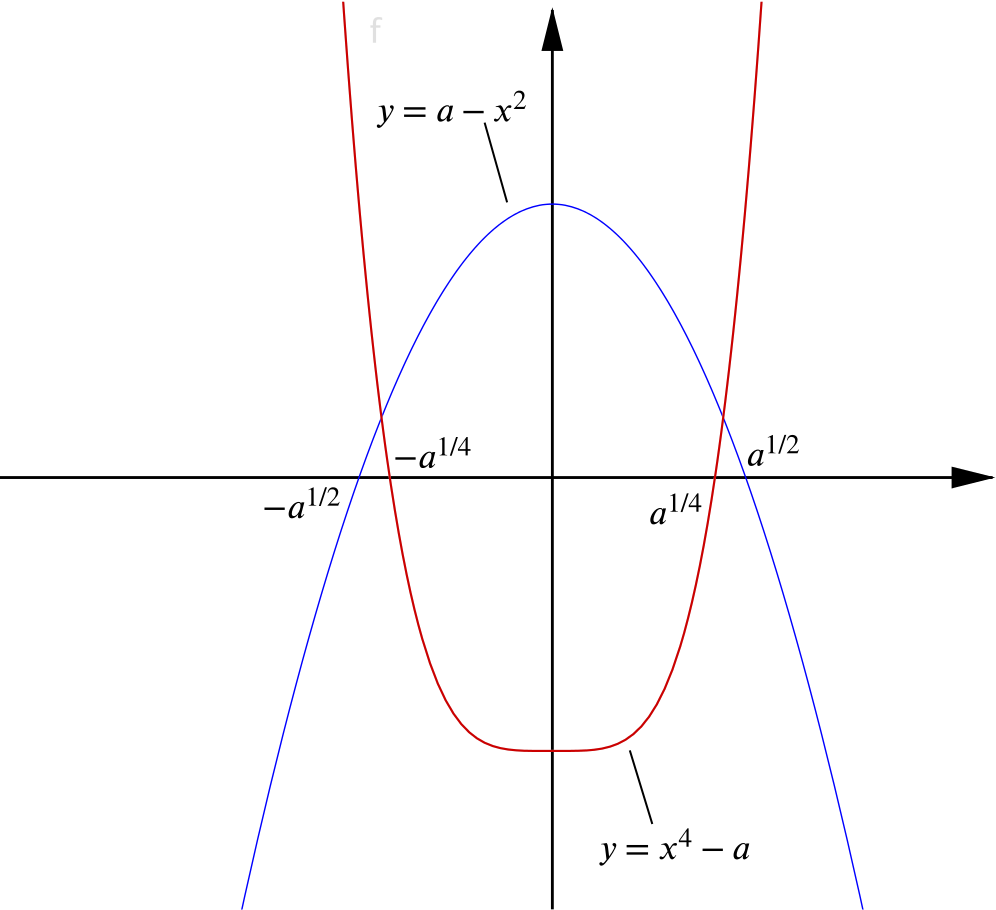
The area of the region bounded by the \(x\)-axis and the curve \(y = f(x)\) is \[\int_{-a^{1/2}}^{a^{1/2}} a - x^2 \:dx = \left[ax-\dfrac{x^3}{3}\right]_{-a^{1/2}}^{a^{1/2}} = \dfrac{4a^{3/2}}{3}.\]
On the other hand the area of the region bounded by the \(x\)-axis and the curve \(y = g(x)\) is \[-\int_{-a^{1/4}}^{a^{1/4}} x^4 - a \:dx = -\left[\dfrac{x^5}{5}-ax\right]_{-a^{1/4}}^{a^{1/4}} = \dfrac{8a^{5/4}}{5}.\]
Since \(5/4<3/2\) it follows that when \(a\) is small, \(\dfrac{8a^{5/4}}{5} > \dfrac{4a^{3/2}}{3}\), but when \(a\) is large, \(\dfrac{8a^{5/4}}{5} < \dfrac{4a^{3/2}}{3}\).
So when are these two areas equal? When \[\dfrac{8a^{5/4}}{5} = \dfrac{4a^{3/2}}{3} \iff a^{1/4}=\dfrac{6}{5} \iff a = \left(\dfrac{6}{5}\right)^4,\] and so the answer is (e).

