The area of the region bounded by the curves \(y = x^2\) and \(y = x + 2\) equals
\(\frac{7}{3}\),
\(\frac{7}{2}\),
\(\frac{9}{2}\),
\(\frac{11}{2}\).
The curves intersect when \(x^2 = x + 2\), or \((x - 2)(x + 1) = 0\), so the points of intersection are at \(x = 2\) and \(x = -1\).
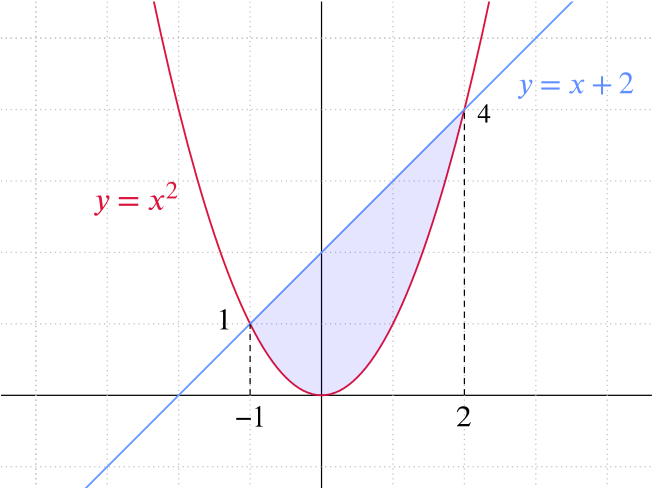
From our sketch we can see that \(x + 2 \geq x^2\) in the region \(-1 \leq x \leq 2\), so
\[\text{Area enclosed} = \left( \text{Area below } \; y = x + 2 \right) - \left(\text{Area below } \; y = x^2 \right) .\]
The area below \(y=x^2\) is calculated by integration, and the area below \(y=x+2\) can be found using the formula for the area of a trapezium. We have \[ \text{Area below } \; y = x + 2 \; = 3 \times \frac{1+4}{2}=\frac{15}{2}, \text{while}\] \[ \text{Area below } \; y = x^2 \; = \int\limits_{-1}^2 x^2 \; dx=\left[\frac{1}{3} x^3\right] _{-1}^2=\frac{8}{3}-\frac{-1}{3}=3.\]
So the area we seek is \[\frac{15}{2}-3=\frac{9}{2}\]
and the answer is (c).
You could also calculate the area under the straight line \(y=x+2\) using the integral \(\int\limits_{-1}^2 x+2 \; dx\).

