Given that \(y = 4x^3 - 7x^2\), find the value of \(dy/dx\) at the point \((2,4)\).
We know that the derivative of \(x^n\) is \(nx^{n-1}\). Using this, we have that \[ \frac{dy}{dx} = y' = 4 \times 3x^2 - 7 \times 2x = 12x^2 - 14x. \] So we have that the value of \(\dfrac{dy}{dx}\) at the point \((2,4)\) is \[ y'(2) = 12 \times 2^2 - 14 \times 2 = 48 - 28 = 20. \]
Hence find the approximate increase in \(x\) which will cause \(y\) to increase from \(4\) to \(4.05\).
Consider the following graph of a curve \(y = f(x)\).
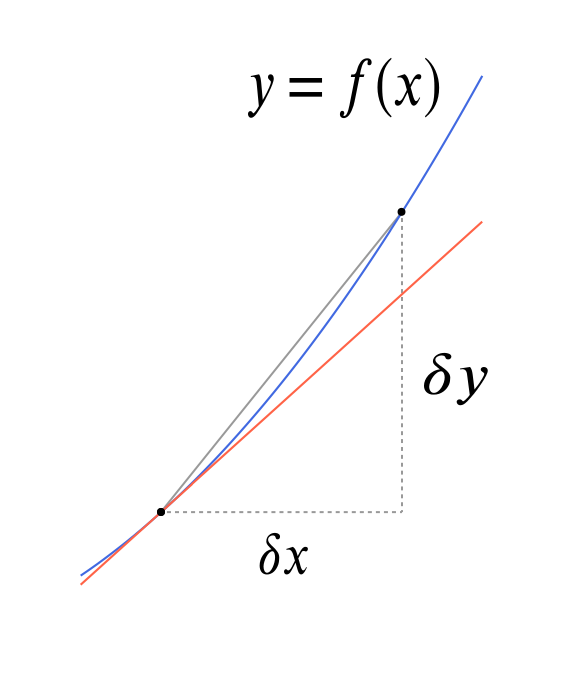
In fact, the definition of \(f'(x_0)\) is the value towards which \[ \frac{f(x_0+\delta x) - f(x_0)}{\delta x} \] tends as \(\delta x\) tends towards zero.
In our case:
- \(f(x) = 4x^3 - 7x^2\),
- \(x_0 = 2\),
- \(f(x_0) = 4\), and
- \(f'(x_0) = 20\).
If we choose \(\delta x\) so that \(f(x_0 + \delta x) = 4.05\), then, from \(\eqref{eq:approximation-to-derivative}\), we would have \[ \frac{4.05 - 4}{\delta x} = \frac{f(x_0+\delta x) - f(x_0)}{\delta x} \approx f'(x_0) = 20, \] and so, by rearranging, \[ \delta x \approx \frac{4.05 - 4}{20} = \frac{1/20}{20} = \frac{1}{400} = 0.0025. \]
If we use our calculators, we find that \[ f(2.0025) - f(2) = 0.05010\ldots, \] and so our approximation is a good one!

