In the region \(0 < x \le 2\pi\), the equation \[\int_0^x \sin(\sin t)\, dt = 0\] has
no solution;
one solution;
two solutions;
three solutions.
Can we evaluate this integral? It looks to be hard - impossible even! Instead, we’ll try to pick up some clues about the shape of \(y = \sin(\sin t)\).
Clue 1. \(\sin(\sin t)=0\) if and only if \(\sin t = 0\), which happens just when \(t = n\pi\), so that’s at \(\pi\) and \(2\pi\) on our interval (and at \(0\)).
Clue 2. \(\sin t\) is positive for \(0 < t < \pi\), taking values from \(0\) to \(1\) on the interval, so \(\sin(\sin t)\) is also positive on this interval, taking values from \(0\) to \(\sin 1\).
Clue 3. \(\sin t\) is negative for \(\pi < t < 2\pi\), taking values from \(0\) to \(-1\) on this interval, so \(\sin(\sin t)\) is also negative on this interval, taking values from \(0\) to \(-\sin 1\).
So the curve has a positive section from \(0\) to \(\pi\), and a negative section from \(\pi\) to \(2\pi\).
Clue 4. The function \(y=\sin t\) is periodic; is \(y = \sin(\sin t)\)? We have \(\sin(\sin(t+2\pi)) = \sin(\sin t)\), so yes, \(\sin(\sin t)\) is periodic.
Could the period be less than \(2\pi\)? Clues 2. and 3. suggest not. We now know the section immediately on the other side of the origin is a negative section.
Clue 5. Could \(\sin(\sin t)\) be odd or even? We have \(\sin(\sin -t) = \sin(-\sin t) = -\sin(\sin t)\), and so \(y=\sin(\sin t)\) is odd, and so has rotational symmetry about the origin.
This must mean that the negative section of the curve from \(-\pi\) to \(0\) matches exactly with the positive section from \(0\) to \(\pi\) (and the section from \(\pi\) to \(2\pi\), by periodicity).
We have enough now to answer the question; the (positive) area below the curve from 0 to \(\pi\) matches exactly with the (negative) area under the curve from \(\pi\) to \(2\pi,\) so there is just one value of \(x\) when the integral is zero (\(x = 2\pi\)) and the answer is (b).
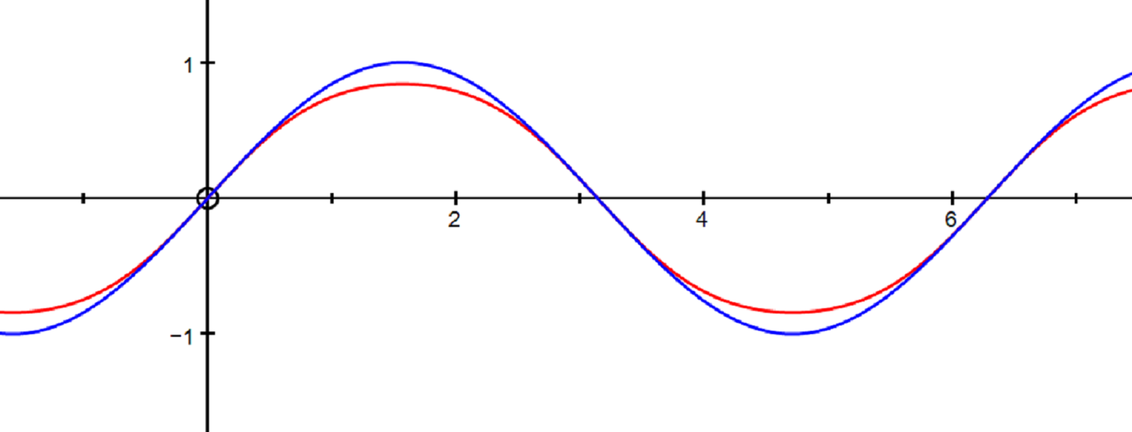
So what does \(y = \sin(\sin t)\) look like? The curve (in red below) is remarkably similar to the curve \(y = \sin t\) (in blue below), but with a lesser amplitude.