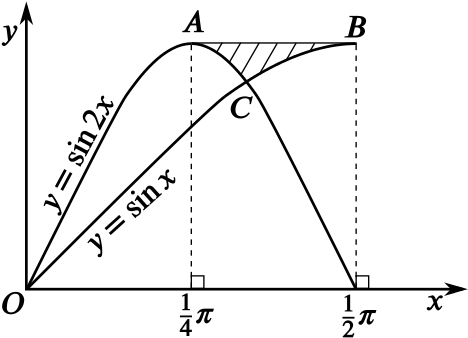
The diagram shows part of the graphs of the curves \(y=\sin 2x\) and \(y=\sin x\).
\(A\) is a maximum point of the curve \(y=\sin 2x\). \(B\) is a maximum point of the curve \(y=\sin x\).
\(C\) is the point of intersection of the curves shown. Find
- the \(x\) co-ordinate of \(C\),
To find the \(x\)-coordinate of \(C\), we need to solve the equation \(\sin x = \sin 2x\) in the region \(0 \le x \le \frac{1}{2}\pi\).
Now \(\sin x = \sin 2x \iff \sin x = 2 \sin x \cos x\). We can see that \(\sin x\) is not zero at \(C\), so the solution we seek is \(\cos x = \dfrac{1}{2}\), and so \(x = \dfrac{\pi}{3}\).
- the shaded area.
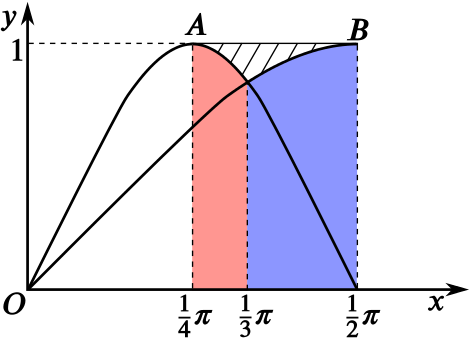
Let’s call the shaded area \(R\). To find \(R\), we start with the area of the rectangle spanned by the line \(AB\) and the \(x\)-axis, which is clearly \(\dfrac{\pi}{4}\).
We then subtract the area below the curves \(y=\sin x\) and \(y=\sin 2x\) as shown by the red area and blue area respectively in the diagram. Thus
\[R=\frac{\pi}{4}-\int_{\pi/4}^{\pi/3} \sin 2x\:dx -\int_{\pi/3}^{\pi/2} \sin x\:dx.\]
Now \[\int_{\pi/3}^{\pi/2} \sin x\:dx = \bigl[-\cos x\bigr]_{\pi/3}^{\pi/2} = \dfrac{1}{2}.\]
And thinking about stretching horizontally \[\int_{\pi/4}^{\pi/3}\sin 2x\:dx = \frac{1}{2}\int_{\pi/2}^{2\pi/3}\sin x\:dx = \frac{1}{2}\bigl[-\cos x\bigr]_{\pi/2}^{2\pi/3} = \dfrac{1}{4}.\]
Thus \[R = \dfrac{\pi}{4}-\dfrac{3}{4}.\]

