Let \[T=\left( \int _{-\pi/2}^{\pi/2}\cos x\,dx\right)\times\left(\int_\pi ^{2\pi} \sin x\,dx\right) \times\left(\int_0^{\pi/8}\frac{dx}{\cos 3x}\right).\] Which of the following is true?
\(T=0\);
\(T<0\);
\(T>0\);
\(T\) is not defined.
We are not asked to work out the exact value of \(T\), only to determine whether it is positive, negative or zero (if it is defined).
It might not be defined if there is a vertical asymptote in the region where we are integrating. We note that \(\dfrac{1}{\cos 3x}\) can be infinite for some values of \(x\).
So we only need to determine the sign for each of the three integrals involved in the product.
Consider the first integral, \[\int_{-\pi/2}^{\pi/2}\cos x\,dx.\] The graph of \(y=\cos x\) looks like this:
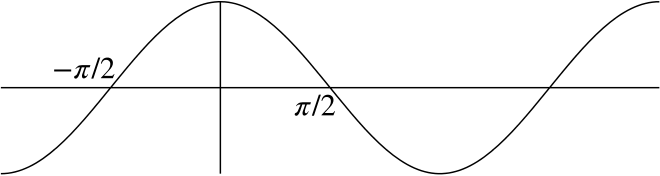
So the integral from \(x=-\pi/2\) to \(x=\pi/2\) is positive, as the graph all lies above the \(x\)-axis in this range.
Then for the second, \[\int_\pi^{2\pi}\sin x\,dx.\] The graph of \(y=\sin x\) looks like this:
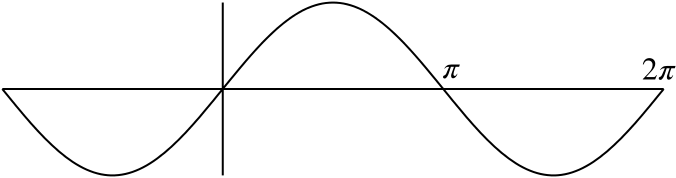
Between \(x=\pi\) and \(x=2\pi\), this graph lies entirely below the \(x\)-axis, so this integral is negative.
For the third integral, \[\int_0^{\pi/8}\frac{dx}{\cos 3x}\] we will need to consider the graph of \(y=\cos 3x\), which is the graph of \(y=\cos x\) stretched by a scale factor of \(\frac{1}{3}\) in the \(x\)-direction.
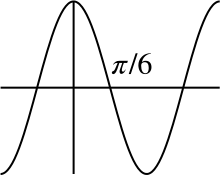
Now \(\frac{1}{\cos 3x}\) is infinite at \(x=\pi/6\), but \(x=\pi/8<\pi/6\), and so there are no vertical asymptotes in the region where we are integrating.
This graph is positive between \(x=0\) and \(x=\pi/8\), so between \(x=0\) and \(x=\pi/8<\pi/6\), we see that \(\dfrac{1}{\cos 3x}\) is positive. Thus this third integral is positive.
Finally, we can combine the three integrals. Since two of them are positive and one is negative, their product must be negative.
The answer is therefore (b), \(T<0\).

