Given the curve \[y = \cos x - \sin x +2\] find in terms of \(a\) an expression for the area \(A\) enclosed between the axes, the ordinate \(a \; (> 0)\) and this curve. Verify that when \(a = 1.5\), \(A = 3.07\) approximately.
The ordinate \(a\) means the line \(x=a\). Our curve lies entirely above the \(x\)-axis. It is something like this.
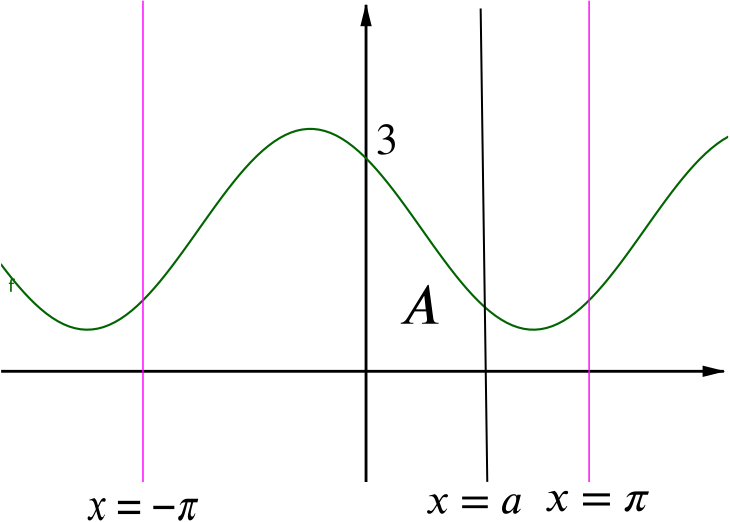
Substituting \(a = 1.5\) gives \(A = 3.0682... \approx 3.07\) as required.
It is required to find the value of \(a\) for which \(A = 3\). Taking \(1.5\) as a first approximation to \(a\), find a second approximation, giving three significant figures in your answer.
So we need to find an approximate solution to \(3 = \sin a + \cos a + 2a -1\) that is better than \(a=1.5\).
There are a number of methods we could use here; decimal search, binary search, linear interpolation, the rearrangement method or simply zooming in with graphing software.
We will use the Newton-Raphson method. This says that given a guess \(x_0\) at the root \(\alpha\) (a solution to \(f(x) = 0\)), then as long as \(x_0\) is reasonably close to \(\alpha\), a better approximation to \(\alpha\) is \(x_1\) where
\[x_1 = x_0 - \dfrac{f(x_0)}{f'(x_0)}.\]
So our equation is \(f(x) = 0\) where \(f(x) = \sin x + \cos x + 2x - 4\), which gives \(f'(x) = \cos x -\sin x + 2\).
Thus \(x_1 = 1.5 - \dfrac{\sin 1.5 + \cos 1.5 + 3 - 4}{\cos 1.5 -\sin 1.5 + 2} = 1.4264...\)
So we have a better approximation to \(a\) than \(1.5\), namely \(1.43\) (\(3\)sf).
Check – \(\sin 1.43 + \cos 1.43 + 2\times 1.43 -1 = 2.99\) (\(3\)sf).

