Using the same axes, sketch the curves \(y = \sin x\) and \(y = \sin 2x\) from \(x = 0\) to \(\tfrac{1}{2}\pi\), where \(x\) is in radians.
The curve \(y = \sin 2x\) has the same shape as \(y = \sin x\), but twice the frequency; we thus have the following sketch.
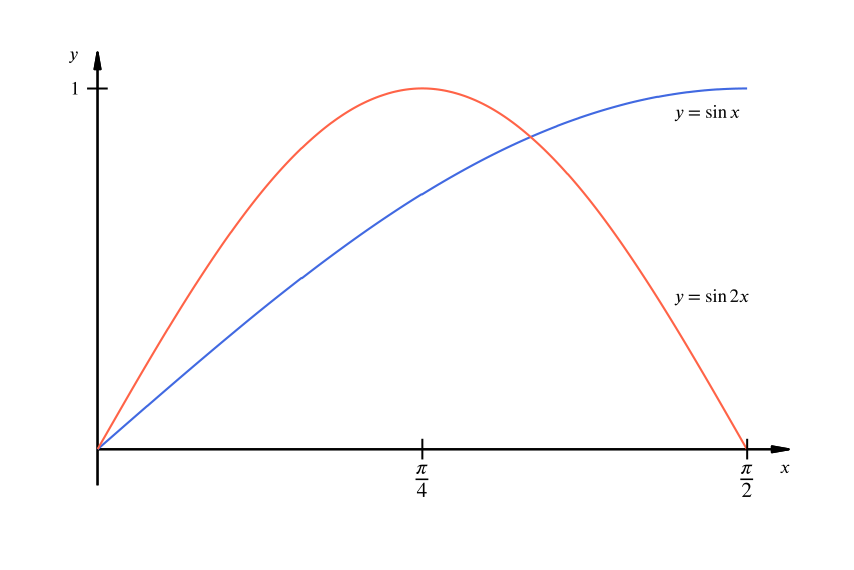
Prove that the curves intersect at the points \[ (0,0) \quad\text{and}\quad \left(\frac{\pi}{3}, \frac{\sqrt{3}}{2} \right). \]
The curves intersect exactly when \(\sin x = \sin 2x\), or \(\sin x = 2 \sin x \cos x\).
This gives us that either \(\sin x = 0\) or \(\cos x = \dfrac{1}{2}\). Within our region this means \(x = 0\) or \(x=\dfrac{\pi}{3}\).
So the curves intersect at \((0,0)\) and at \(\left(\dfrac{\pi}{3}, \dfrac{\sqrt{3}}{2}\right)\).
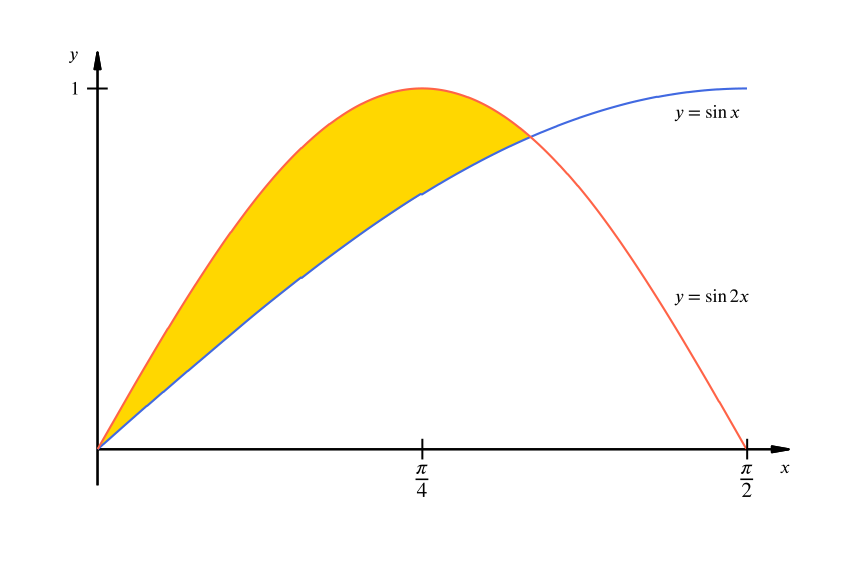
Calculate the area of the region bounded by the parts of the curves between these two points.
The area we are to calculate is the yellow area indicated in the following diagram.
Thinking about scaling
We are looking for the area\[\begin{align*} A &= \int_0^{\dfrac{\pi}{3}} \sin 2x\:dx - \int_0^{\dfrac{\pi}{3}}\sin x\:dx\\ &= \frac{1}{2}\int_0^{\dfrac{2\pi}{3}} \sin x\:dx - \int_0^{\dfrac{\pi}{3}}\sin x\:dx\\ &= \frac{1}{2}\biggl[-\cos x\biggr]_0^{\dfrac{2\pi}{3}} - \biggl[-\cos x\biggr]_0^{\dfrac{\pi}{3}}\\ &= \frac{1}{2}\left(\frac{1}{2}+1\right) - \left(-\frac{1}{2}+1\right)\\ &= \frac{1}{4}. \end{align*}\]
Using an implicit substitution
We are looking for the area\[\begin{align*} A &= \int_0^{\dfrac{\pi}{3}} \sin 2x -\sin x\:dx \\ &= \biggl[ -\frac{\cos 2x}{2}+\cos x \biggr]_0^{\dfrac{\pi}{3}} \\ &= \frac{1}{4} + \frac{1}{2} + \frac{1}{2}-1\\ &= \frac{1}{4}. \end{align*}\]

