Find the equation of the normal to the parabola \(y^2=4ax\) at the point \((at^2,2at)\).
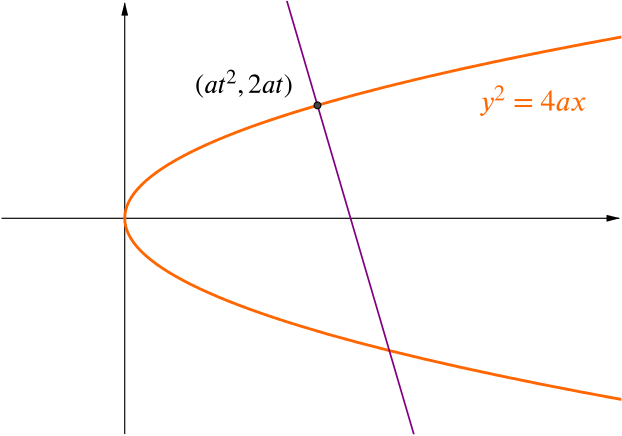
Approach 1: differentiate with respect to the parameter \(t\).
Differentiating with respect to \(t\), we see \(\dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt}= \dfrac{2a}{2at}= \dfrac{1}{t}\).
So the gradient of the normal at \(T\) is \(-t\).
The point \((at^2,2at)\) is on the line which gives us its equation as \(y = -tx +at^3+2at\).
Approach 2: find \(y\) directly
We have \(y=2\sqrt{ax}\) (taking the positive square root for the top half of the curve).
Now we can differentiate to find \(\dfrac{dy}{dx} = 2\cdot\dfrac{1}{2}(ax)^{-1/2}a= \sqrt{\dfrac{a}{x}}\), and at \(x=at^2\) (noting that \(t\) is positive), this gives us \(\dfrac{dy}{dx} = \dfrac{1}{t}\). As above, we conclude the normal has gradient \(-t\).
We get the same result for the bottom half of the curve.
Approach 3: implicit differentiation
Differentiating \(y^2=4ax\) with respect to \(x\) gives, using the chain rule, \[2y \dfrac{dy}{dx} = 4a\] and therefore the gradient at \((at^2,2at)\) is \(\dfrac{4a}{2y} = \dfrac{4a}{4at}=\dfrac{1}{t}\).
Prove that, if \(p^2>8\), two chords can be drawn through the point \((ap^2,2ap)\) which are normal to the parabola at their second points of intersection, and that the line joining these points of intersection meets the axis of the parabola in a fixed point, independent of \(p\).
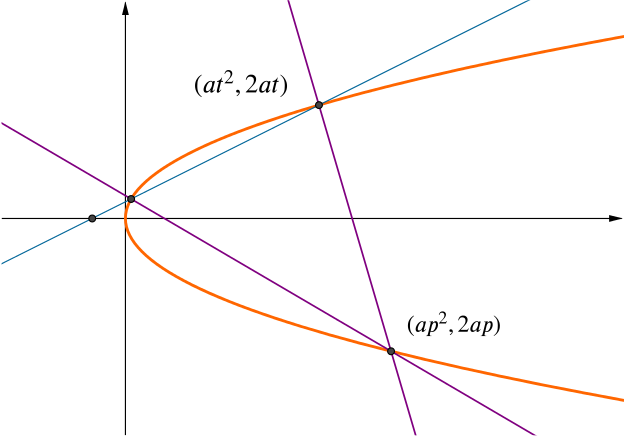
We seek points \(T = (at^2, 2at)\) where the normal at \(T\) passes through \(P = (ap^2, 2ap)\).
So we need \((ap^2,2ap)\) to lie on the line \(y = at^3+2at-xt\).
Substituting in these values of \((x,y)\) we obtain \[2ap = at^3 + 2at-ap^2t\] or (cancelling the \(a\)) \[t^3 + (2-p^2)t - 2p = 0.\]
We already know one solution: \(p=t\) (because the normal at the point given by \(p\) passes through the curve at this same point.)
So we can take out from this cubic a factor of \((p-t)\) to give \[t^2 + pt + 2 = 0.\]
A quadratic has two roots if and only if its discriminant is positive, or “\(b^2-4ac>0\)”, which here gives simply \(p^2-8>0\), as required.
Finally, we consider the line joining \(T_1=(at_1^2,2at_1)\) and \(T_2=(at_2^2,2at_2)\) on the parabola (where \(t_1\) and \(t_2\) denote the two roots of the quadratic).
We want to find where this intersects the axis of the parabola, the line \(y=0\).
The gradient of the line is given by ‘the difference in \(y\) coordinates divided by the difference in \(x\) coordinates’, which is \[\frac{2a(t_2-t_1)}{a(t_2^2-t_1^2)} = \frac{2}{t_1+t_2}.\]
Hence the equation of the line is \[y - 2at_1 = \frac{2}{t_1+t_2} (x - a t_1^2),\] and by setting \(y=0\) we find \[x = at_1^2 + \frac{1}{2} (t_1+t_2)(-2at_1) = -at_1t_2.\]
We can recall now that the product of the roots of the quadratic \(x^2 + ax + b = 0\) is given by \(b\), the constant term.
But in \(t^2+pt+2=0\) the constant term is simply \(2\), giving the \(x\)-intercept to be \(x = -2a\), which is indeed independent of \(p\).

