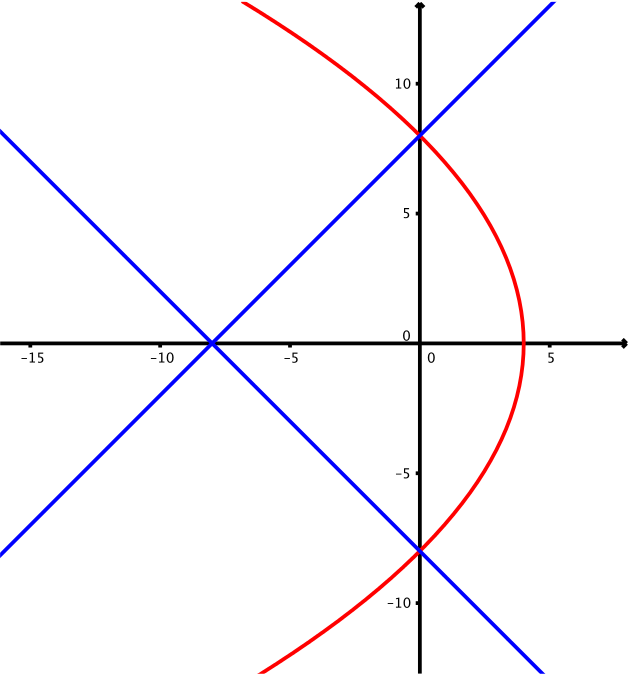
A curve is given parametrically by the equations \[x=4-t^2, y=4t.\]
Find the equations of the normals to the curve at the points where the curve meets the \(y\)-axis. Show that these normals meet on the \(x\)-axis.
The curve meets the \(y\)-axis where \(x=0\), hence at \(t=\pm 2\). The corresponding points on the curve are \(P= (0,8)\) and \(Q= (0,-8)\).
Differentiating we find \(\dfrac{dy}{dt} = 4\) and \(\dfrac{dx}{dt} = -2t\). By the Chain Rule, \[\dfrac{dy}{dx} = \dfrac{dy/dt}{dx/dt} = -\dfrac{2}{t} ,\] so the gradient of the normal at the point given by the parameter \(t\) is \(\dfrac{t}{2}\).
The normal at \(P\) is \(y = x + 8\), and the normal at \(Q\) is \(y = -x - 8\).
Setting the two equations equal to each other gives \(-x-8=x+8 \implies x=-8 \implies y=0\), and hence the lines meet on the \(x\)-axis.
The curve is a parabola, symmetrical about the \(x\)-axis. The symmetry of the situation guarantees that the normals will meet on the \(x\)-axis.