It is given that the two curves \[y=4-x^2 \qquad \text{and} \qquad mx=k-y^2,\] where \(m>0\), touch exactly once.
- In each of the following four cases, sketch the two curves on a single diagram, noting the coordinates of any intersections with the axes:
The first equation, \(y = 4-x^2\) does not involve \(k\) and \(m\), so this curve does not vary.
We can rearrange the second curve, \(mx=k-y^2\), into the form \(x=-\dfrac{y^2}{m}+\dfrac{k}{m}\) and see that we have a quadratic curve in \(y\), a ‘vertex-right’ parabola, with an \(x\)-intercept of \(\dfrac{k}{m}\) and \(y\)-intercepts of \(\pm\sqrt{k}\).
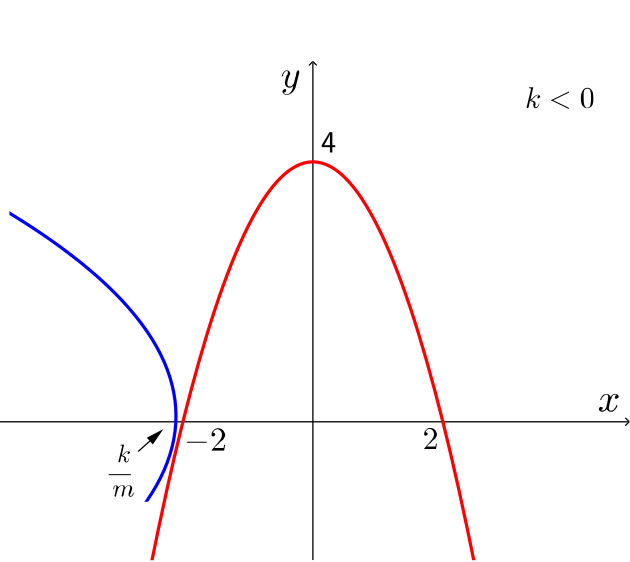
- \(k<0\);
The curves touch in the third quadrant, and do not intersect anywhere else.
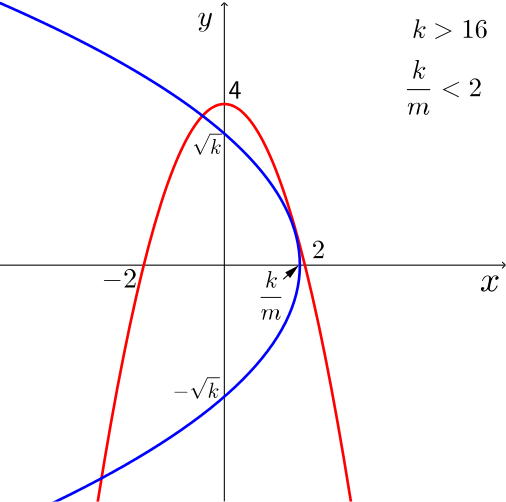
- \(0< k <16\), \(k/m<2\);
The curves touch in the first quadrant, and also intersect in the second and third quadrants.
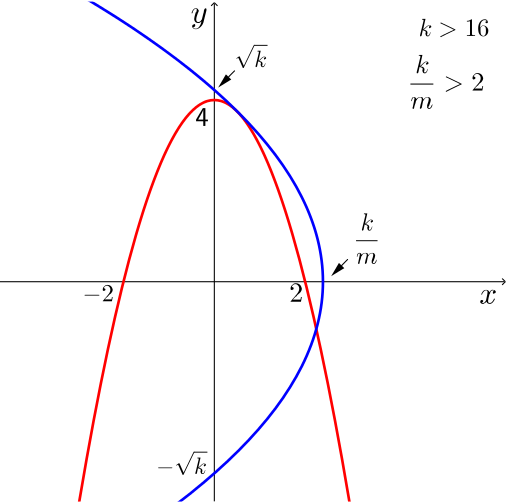
- \(k>16\), \(k/m>2\);
The curves touch in the first quadrant, and also intersect in the third and fourth quadrants.
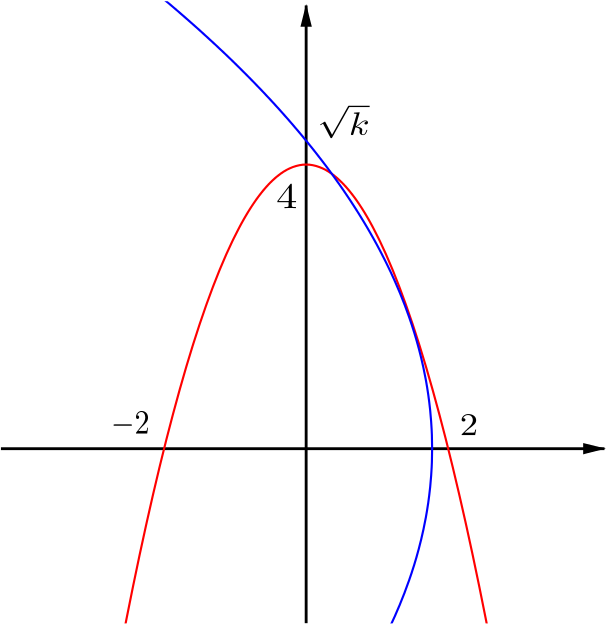
- \(k>16\), \(k/m<2\).
The curves touch in the first quadrant and also intersect in the first and third quadrants.
- Now set \(m = 12\). Show that the \(x\)-coordinate of any point at which the two curves meet satisfies \[x^4-8x^2+12x+16-k=0.\]
Let \(a\) be a value of \(x\) at the point where the curves touch. Show that \(a\) satisfies \[a^3-4a+3=0\] and hence find the three possible values of \(a\).
as required.
This can be found without calculus. Solving \(y=4-x^2\) and \(12x=k-y^2\) together gives \(x^4-8x^2+12x+16-k=0.\)
If we now equate this to \((x-a)^2(x-b)(x-c)=0\) (we have a double root at \(a\)), equate coefficients, and eliminate \(b, c\) and \(k\), we get \(a^3-4a+3=0.\)
By inspection, \(a=1\) is a solution, so we take out \(a-1\) as a factor and get \[(a-1)(a^2+a-3)=0.\] The roots of the quadratic are \[a=\frac{-1\pm\sqrt{13}}{2},\] so the possible values of \(a\) are \[1,\,-\frac{1}{2}\pm\frac{1}{2}\sqrt{13}.\]
Derive also the equation \[k=-4a^2+9a+16.\]
where we’ve used \(a^3=4a-3\) from the previous part to eliminate the \(a^4\) term.
Which of the four sketches in part (i) arise?
When \(a=1\), we have \(k=16+9-4=21>16\) and \(\dfrac{k}{m}=\dfrac{21}{12}<2\). This is therefore case (d).
Now \(a=\dfrac{-1+\sqrt{13}}{2} \approx 1.30 \implies k \approx 20.9 > 16\), and \(\dfrac{k}{m} \approx \dfrac{20.9}{12}<2\), and so we have situation (d).
On the other hand, \(a=\dfrac{-1-\sqrt{13}}{2} \approx -2.30 \implies k \approx -25.9\), and so we have situation (a).
It’s worth noting that two of the values of \(k\) we have here are very close to each other, \(k = 21\), and \(k \approx 20.9\).
Try zooming in on these two solutions using the GeoGebra applet below.

