A hollow container is to be made out of a fixed total area \(\pi a^2\) of sheet metal and its shape is to be that of a right circular cone completed by the circular base on which it stands. Find the radius of the base when the container encloses maximum volume.
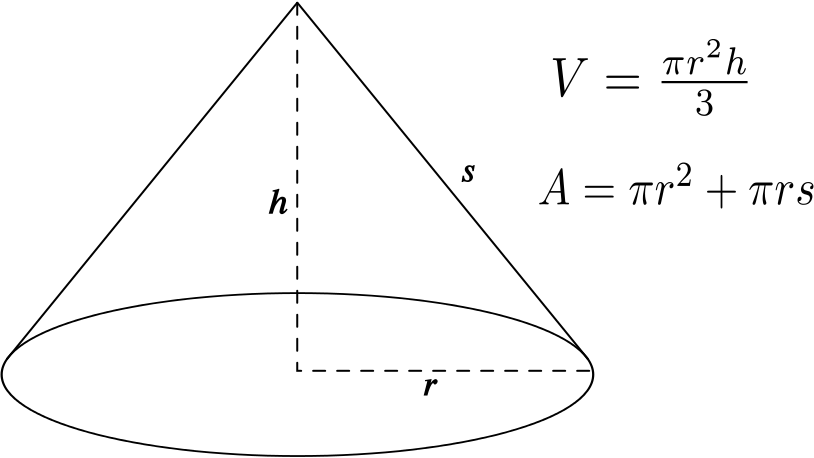
The surface area \(A\) of a cone with radius \(r\) and height \(h\) is given by \(A=\pi r^2 + \pi s r\), where \(s=\sqrt{h^2 + r^2}\) is the sloped side of the cone.
The \(\pi r^2\) part comes from the base of the cone. The other part when laid flat is a sector with radius \(s\) and arclength \(2\pi r\).
If the angle in the sector is \(\theta\), then \(s\theta = 2\pi r\). The area of the sector is \(\dfrac{1}{2}s^2 \theta\), which on eliminating \(\theta\) is \(\pi s r\), as above.
We know that this area is \(\pi a^2\), hence
\[\begin{align*} \pi a^2 &= \pi r^2 + \pi s r\\ a^2 -r^2 &= \sqrt{h^2r^2 + r^4}\\ \sqrt{\frac{a^4}{r^2} - 2a^2} &= h. \end{align*}\] Now the volume of a cone is \(V=\dfrac{\pi}{3} h r^2\), which gives \[\begin{align*} V=\frac{\pi}{3} \sqrt{a^4r^2 - 2a^2r^4}. \end{align*}\] To find when the volume is a maximum, we differentiate and set the first derivative equal to zero. We’ll use the substitution \(u=a^4r^2 - 2a^2r^4\) and the Chain Rule. \[\begin{align*} V &= \frac{\pi}{3}u^{\frac{1}{2}} \\ \frac{dV}{dr} = \frac{dV}{du}\times\frac{du}{dr} &= \frac{\pi}{6}u^{-\frac{1}{2}}\left(2a^4r-8a^2r^3\right) \\ &= \frac{\pi}{3}\frac{a^4r-4a^2r^3}{\sqrt{a^4r^2-2a^2r^4}} \end{align*}\] This is zero when \[\begin{align*} a^4r-4a^2r^3 &= 0\\ a^2r\left(a^2-4r^2\right) &= 0\\ r=0 \text{ or } \frac{a}{2}. \end{align*}\]Note that we can ignore the negative solution, \(r=-\frac{a}{2}\), because of the physical context of the question.
Finding the second derivative of the volume (to show we have a maximum) would be difficult.
Instead we could argue that \(V=0\) for \(r=0\) and \(r=\dfrac{a}{\sqrt{2}}\), and is positive for all values of \(r\) in between. The turning point at \(r=\dfrac{a}{2}\) must therefore be a maximum.

