Express \(\dfrac{3x}{(x-1)(x+2)}\) in partial fractions.
Let \[\frac{3x}{(x-1)(x+2)} = \frac{A}{x-1} + \frac{B}{x+2}\]
Then by multiplying through by \((x-1)(x+2)\), we have \[3x = A(x+2) + B(x-1).\]
If we let \(x = 1\), then our equation becomes \[\begin{align*} 3 = 3A, \\ \text{so} \qquad A = 1. \end{align*}\] If we now choose to use \(x = -2\), then we have \[\begin{align*} -6 = -3B, \\ \text{so} \qquad B = 2. \end{align*}\]Alternatively, we can compare coefficients.
So we have \[\frac{3x}{(x-1)(x+2)} = \frac{1}{x-1} + \frac{2}{x+2}.\]
Show that \(\dfrac{dy}{dx}\) is negative at all points on the graph of \[y=\frac{3x}{(x-1)(x+2)}.\]
We differentiate the partial fractions to obtain \[\frac{dy}{dx} = -\frac{1}{(x-1)^2} - \frac{2}{(x+2)^2}.\]
We can see that this must be negative at all points, because each term is negative.
The gradient is not defined at \(x = 1, -2\).
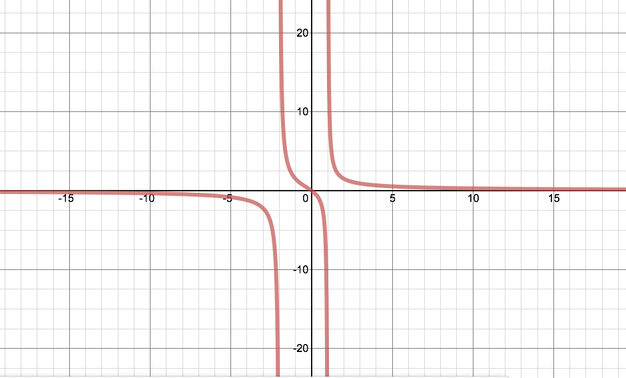
Sketch this graph, showing the two asymptotes parallel to the \(y\)-axis and the asymptote perpendicular to the \(y\)-axis.
When \(x = 0\), \(y = 0\). There are no other points where the curve crosses the axes.
The two asymptotes parallel to the \(y\)-axis are \(x=1\) and \(x=-2\).
We have determined that \(\dfrac{dy}{dx}\) is always negative, and so it cannot equal \(0\), and thus there are no stationary points.
We also observe that as \(x\rightarrow \pm \infty\), \(y\rightarrow 0\).
We can now confidently sketch the graph:
By sketching on the same diagram a second graph (the equation of which should be stated), or otherwise, find the number of real roots of the equation \[(x-1)(x+2)(x+3)=3x.\]
We observe that the equation can be rearranged to \[x+3=\frac{3x}{(x-1)(x+2)},\] which suggests sketching the graph \(y=x+3\) onto the original graph.

There are three points of intersection for the two graphs, so there are three real roots for the equation \((x-1)(x+2)(x+3)=3x\).

