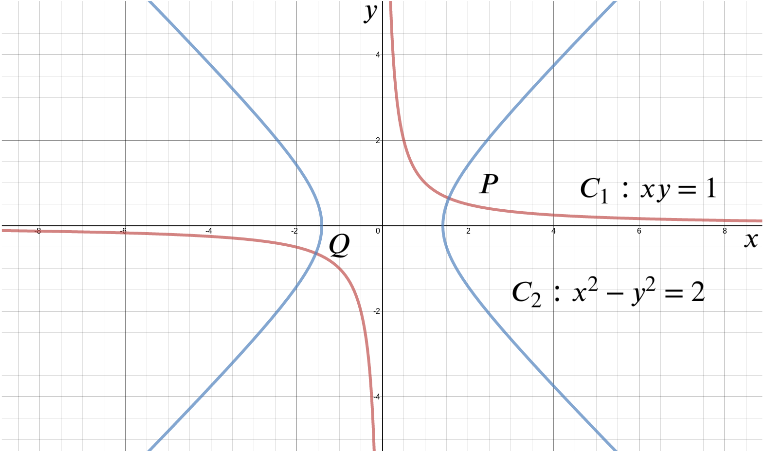
Note that \(C_2\) does not intersect the \(y\)-axis.
The curves intersect at \(P\) and \(Q\). Given that the coordinates of \(P\) are \((a,b)\) (which you need not evaluate), write down the coordinates of \(Q\) in terms of \(a\) and \(b\).
If \(P\) has coordinates \((a,b)\), then \(Q\) has coordinates \((-a,-b)\).
This is easily checked by substituting back into the equations for \(C_1\) and \(C_2\).
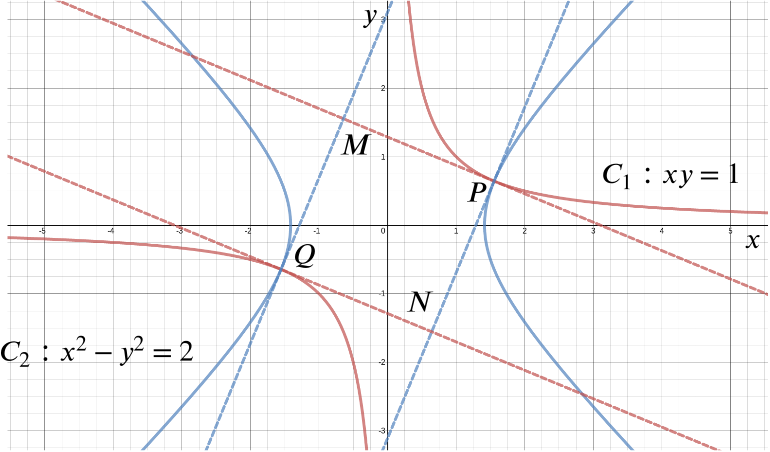
The tangent to \(C_1\) through \(P\) meets the tangent to \(C_2\) through \(Q\) at the point \(M\), and the tangent to \(C_2\) through \(P\) meets the tangent to \(C_1\) through \(Q\) at \(N\). Show that the coordinates of \(M\) are \((-b,a)\) and write down the coordinates of \(N\).
The gradient of \(C_1\) at any point is given by: \[y+x\frac{dy}{dx}=0 \quad \Longrightarrow \quad \frac{dy}{dx}=-\frac{y}{x}.\] Similarly, the gradient of \(C_2\) at any point is given by \[2x-2y\frac{dy}{dx}=0 \quad \Longrightarrow \quad \frac{dy}{dx}=\frac{x}{y}.\] Thus the tangent to \(C_1\) at \(P(a,b)\) has equation \[y-b=-\frac{b}{a}(x-a),\] while the tangent to \(C_2\) at \(Q(-a,-b)\) has equation \[y+b=\frac{a}{b}(x+a).\]
The intersection of these two lines is at \(M\), so we solve the equations simultaneously to find the coordinates of \(M\).
at some point.
We want to solve \[\frac{a}{b}x + \frac{a^2 - b^2}{b} = -\frac{b}{a}x + 2b.\] Multiplying through by \(ab\), we can eliminate denominators, and since \(ab = 1\) we do not need to change the last term. We can also replace \(a^2 - b^2\) by \(2\). We get \[a^2 x + 2a = -b^2 x + 2b,\] so \[(a^2 + b^2)x = 2(b-a).\]
We want to deal with \(a^2 + b^2\). We could try to write it in terms of \(b-a\), since that’s on the right-hand side.
We have \[a^2 + b^2 = (a - b)^2 + 2ab = (a-b)^2 + 2,\] so the above equation becomes \[[(a-b)^2 + 2]x = 2(b-a).\]
We can divide through by \(a-b\) (it cannot be zero because \(a^2 - b^2 = 2\)), and use \(a^2 - b^2 = 2\) to give \(\frac{2}{a-b} = a+b\), using the familiar difference of two squares.
Thus the equation becomes \[\left((a-b) + \frac{2}{a-b}\right) x = -2,\] that is, \[(a - b + a + b) x = -2.\] Now we can tidy up to get \[x = -\frac{1}{a} = -b,\] and using either of the equations of the tangents, say the first one, then gives \[y = \frac{b^2}{a} + 2b = \frac{b^2 + 2ab}{a} = \frac{b^2 + 2}{a} = a.\]
So \(M\) has coordinates \((-b,a)\), as required.
Then we see immediately that \(N\) has the coordinates \((b,-a)\).
Show that \(PMQN\) is square.
and note that \[-\frac{b}{a}\times\frac{a}{b}=-1.\] The tangent of \(C_2\) at \(P\) is therefore also the normal of \(C_1\) at \(P\). By an analogous argument around \(PMQN\) all intersecting straight lines meet at right angles.
All we then need to do is show that one of the side lengths is equal to any one of the others, and indeed we have \[\vert PM \vert = \sqrt{(a--b)^2+(b-a)^2}=\sqrt{2(a^2+b^2)}\] and \[\vert QN \vert = \sqrt{(-a-b)^2+(-b--a)^2}=\sqrt{2(a^2+b^2)}.\]
Thus \(PMQN\) is a square.

