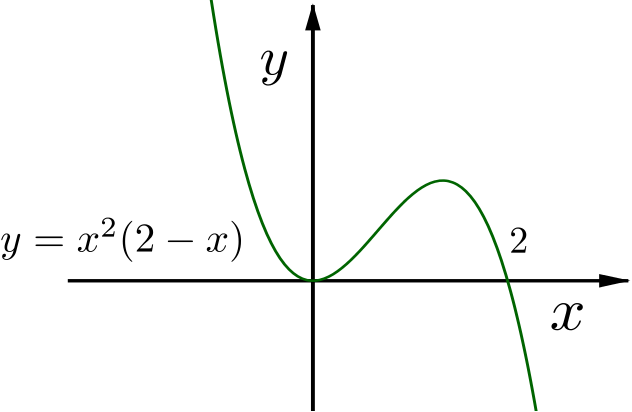
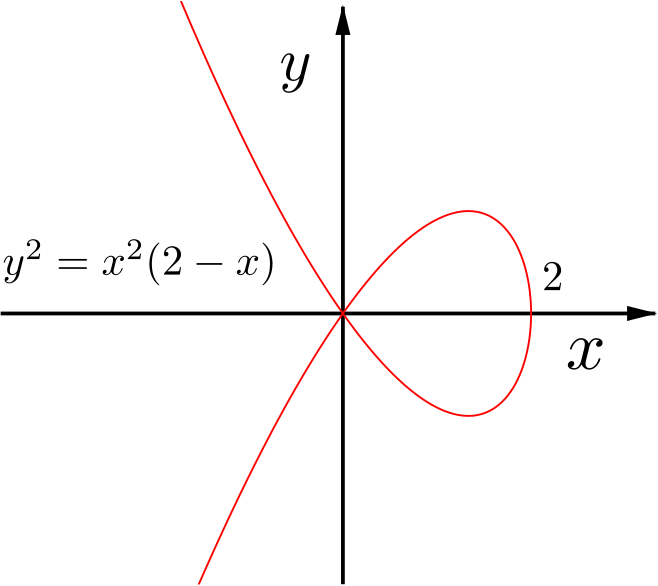The polynomial on the right-hand side has a double zero at the origin and a zero at \(x = 2\).
Further, \[\begin{equation*} \frac{dy}{dx} = -3x^2 + 4x = x(4-3x) \end{equation*}\]so the curve has two stationary points, at \(x = 0\) and \(x = \dfrac{4}{3}\).
Since the leading term of the polynomial is \(-x^3\), \(y \to \infty\) as \(x \to -\infty\), and \(y \to -\infty\) as \(x \to \infty\).
Consequently, the first stationary point must be a local minimum and the second stationary point must be a local maximum.
This information, when put together, leads to the following sketch.
indicating briefly how the form of the curve has been derived.
Firstly, note that this curve does not exist where the right hand side is negative, that is when \(x>2\). This corresponds to where the curve in the first part of the question is below the \(x\)-axis.
For other values of \(x\), the curve has two branches, \(y=\pm x\sqrt{2-x}\).
The curve cuts or touches the \(x\)-axis at \(x=0\) and at \(x=2\).
So we have some kind of loop above and below the \(x\)-axis between \(x=0\) and \(x=2\), while for \(x<0\) the curve is in two branches, one increasing and the other decreasing.
In order to discover the nature of the axis crossings, we could think about how \(y=\sqrt{2-x}\) behaves and what happens when we multiply it by \(x\). Alternatively, we can do some calculus.
Differentiating implicitly we find \[\begin{align*} y^2 &=2x^2-x^3 \\ \implies\quad 2y\frac{dy}{dx} &= 4x-3x^2 \\ \iff\quad \frac{dy}{dx} &=\frac{4x-3x^2}{2y} \end{align*}\]As \(x\) approaches \(2\), \(y\to 0\) and \(\frac{dy}{dx}\to\frac{8-12}{2y}\to\pm\infty\). So a tangent to the curve at \(x=2\) would be vertical.
We can’t evaluate \(\frac{dy}{dx}\) at the origin, but nearby \(x\) is very small so \(y^2\approx2x^2\). This means that \(y\approx\pm\sqrt{2}x\) and we have \[\frac{dy}{dx}\approx\frac{4x-3x^2}{\pm 2\sqrt{2}x} \approx \pm\sqrt{2}.\] Hence the curve passes through the origin with gradient \(\pm\sqrt{2}\).
We are led, then, to the following sketch.