A curve has parametric equations \(x=5a\sec\theta,\,y=3a\tan\theta\), where \(-\frac{1}{2}\pi < \theta < \frac{1}{2}\pi\) and \(a\) is a positive constant. Find the coordinates of the point on the curve at which the normal is parallel to the line \(y=x\).
Thus \[\frac{dy}{dx}=\frac{3a\sec^2\theta}{5a\sec\theta\tan\theta}=\frac{3}{5\sin\theta}.\]
The normal to the curve therefore has gradient \[-\frac{5}{3}\sin\theta.\]
The normal is parallel to \(y=x\) when \[-\frac{5}{3}\sin\theta=1\quad \Longrightarrow \quad \sin\theta=-\frac{3}{5}.\]
By sketching a graph of \(y=\sin\theta\), we can see that there’s a unique value of \(\theta\) in the range \(-\dfrac{\pi}{2}<\theta<\dfrac{\pi}{2}\) for which \(\sin\theta=-\dfrac{3}{5}\).
The blue line in the diagram shows that this corresponds to a positive value of \(\cos\theta\).
Hence, we get that \[\cos^2 \theta = 1 - \sin^2 \theta = 1 - \left(-\frac{3}{5}\right)^2 = \frac{16}{25} \quad \Longrightarrow \quad \cos \theta = \frac{4}{5}\] as \(\cos\theta\) is positive.
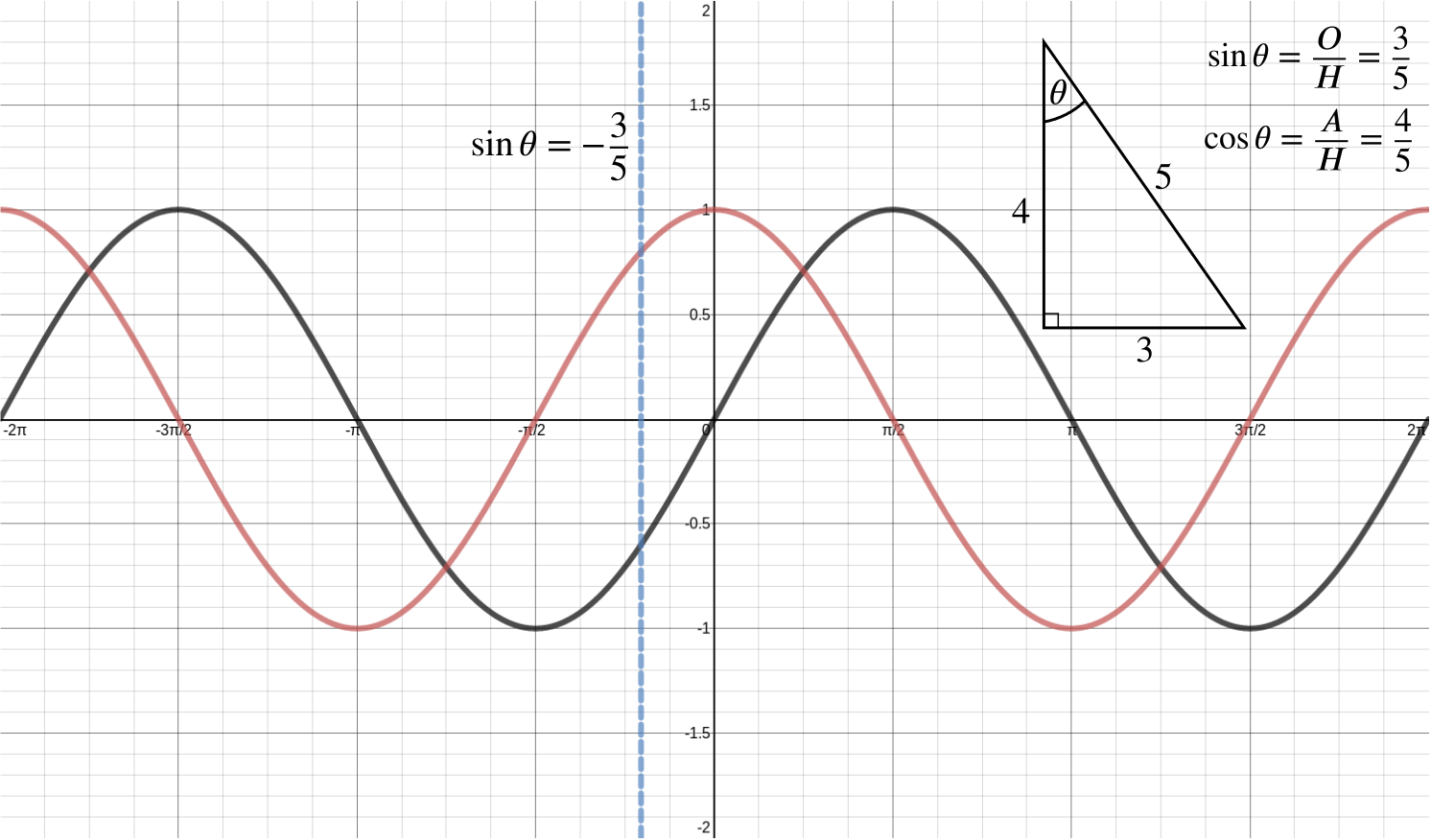
Alternatively, using the sketch above, we can see that we are dealing with a \(3-4-5\) triangle, and so the value of cosine we need is \(\cos\theta=\dfrac{4}{5}\).

