Where does this tangent to this ellipse meet $x=a$?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Let us denote the coordinates of \(P\) by \((p, q)\).

Since \(P\) is in the first quadrant we have \(p, q > 0\), and since \(P\) lies on the ellipse we know that \[\begin{equation} \frac{p^2}{a^2} + \frac{q^2}{b^2} = 1. \label{eq:ellipse-eqn-eval-at-P} \end{equation}\] Let us first work out the equation for the tangent to the ellipse at \(P\) in the form \(y = mx + c\). Differentiating implicitly we have \[\frac{2x}{a^2} + \frac{2y}{b^2} \frac{dy}{dx} = 0\] and hence \(\dfrac{dy}{dx} = - \dfrac{x b^2}{y a^2}\). The value of \(m\) is the value of this derivative at the point \((p, q)\), which is \(m = - \dfrac{p b^2}{q a^2}\). We also know that the point \(P\) lies on the tangent and hence we have the condition \[q = - \frac{p^2 b^2}{q a^2} + c\] which is equivalent to \[c = \frac{q^2 a^2 + p^2 b^2}{q a^2}.\] Using \(q^2 a^2 + p^2 b^2 = a^2 b^2\), which follows directly from the above equation \(\eqref{eq:ellipse-eqn-eval-at-P}\), the tangent is described by \[\begin{equation} y = - \frac{p b^2}{q a^2} x + \frac{b^2}{q}. \label{eq:equation-of-tangent-at-P} \end{equation}\]

Let us now work out the coordinates of the point \(T\) shown in the following picture.

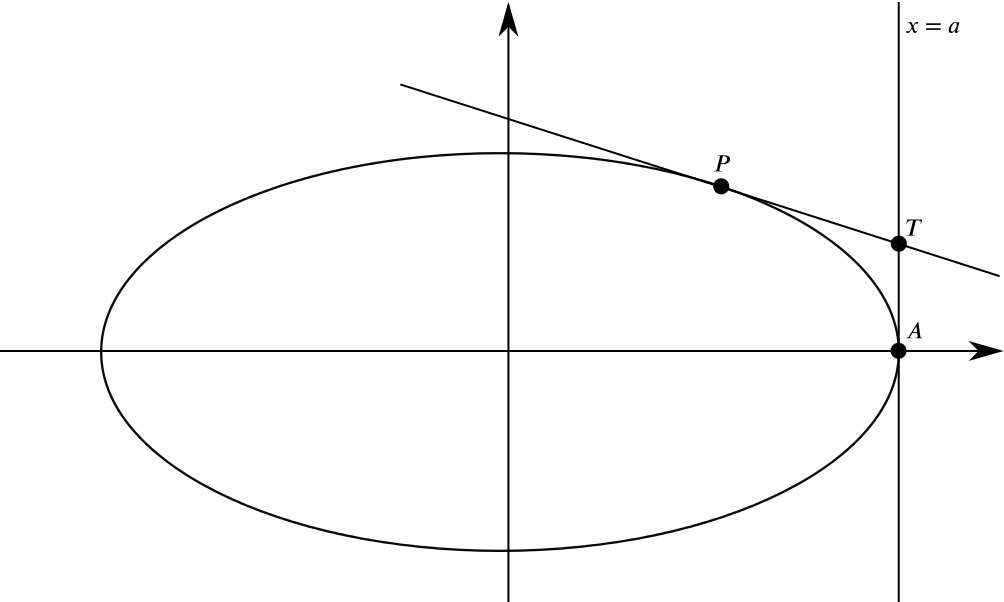
We can get the \(y\)-coordinate by inserting \(x = a\) into the equation of the tangent at \(P\). We get \[y = - \frac{p b^2}{q a^2}a + \frac{b^2}{q} = \frac{a b^2 - p b^2}{q a}\] and hence \(T\) has the coordinates \(\left(a, \dfrac{a b^2 - p b^2}{q a}\right)\).

We will now calculate the coordinates of the point \(R\) drawn in the following picture.

We start off by computing the equation for the line \(A^{\prime} P\). Since the coordinates of \(P\) are \((p, q)\), the slope of the line is given by \(\dfrac{q}{p + a}\) and hence the line is of the form \(y = \dfrac{q}{p + a} x + c\) for the \(y\)-axis intercept \(c\). Using that the point \(A^{\prime}\) lies on the line we get the condition \(- \dfrac{q a}{p + a} + c = 0\) and hence \(c = \dfrac{q a}{p + a}\). Thus the line \(A^{\prime} P\) has the equation \[\begin{equation} y = \frac{q}{p + a} x + \frac{q a}{p + a}. \label{eq:equation-Aprime-P} \end{equation}\]

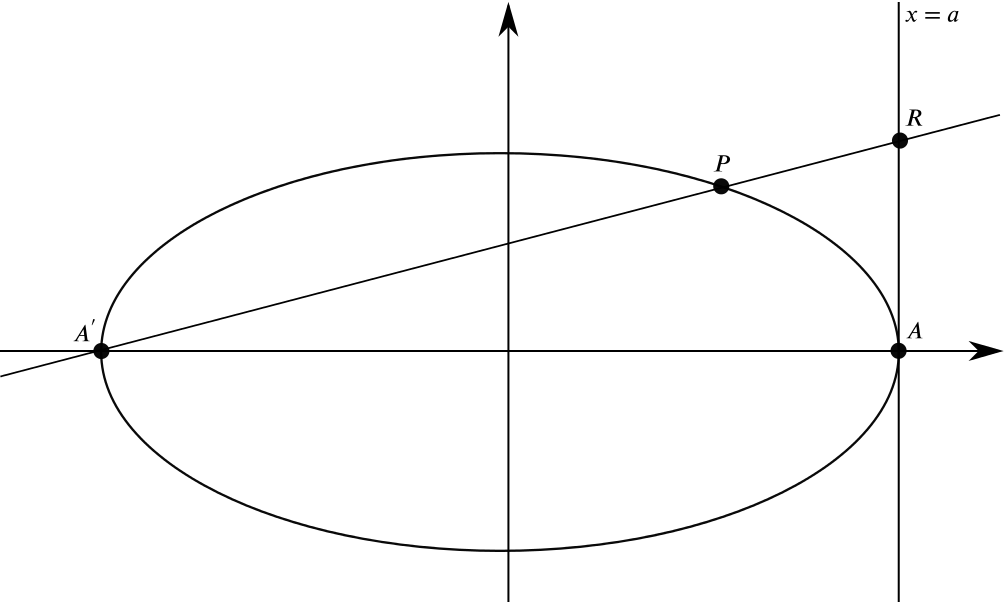
Since the \(x\)-coordinate for \(R\) is \(a\) we can compute the \(y\)-coordinate via \[y = \frac{q a}{p + a} + \frac{q a}{p + a}.\] and hence the point \(R\) has the coordinates \(\left(a, 2\dfrac{q a}{p + a}\right)\).

Since the points \(A\), \(T\), and \(R\) all lie on the same vertical line \(x = a\) it suffices to show that \(T\) lies exactly in the middle of \(A\) and \(R\), i.e. that the \(y\)-coordinate of \(T\) is half the \(y\)-coordinate of \(R\). From equation \(\eqref{eq:ellipse-eqn-eval-at-P}\) we get \(b^2 = \dfrac{q^2 a^2}{a^2 - p^2}\). Thus we have \[\begin{align*} b^2 \frac{a - p}{q a} &= \dfrac{q^2 a^2}{a^2 - p^2} \frac{a - p}{q a} \\ &= \frac{qa(a-p)}{a^2 - p^2} \\ &= \frac{qa(a-p)}{(a+p)(a-p)} \\ &= \frac{qa}{a+p} \end{align*}\]

and hence \(AT = TR\).

Let us now compute the coordinates of the points \(Q\) and \(M\) shown in the following drawing.

The \(y\)-coordinate of \(Q\) is given by the \(y\)-axis intercept of the tangent to the ellipse at \(P\). We have already found the intercept as part of equation \(\eqref{eq:equation-of-tangent-at-P}\), so we already know that the point \(Q\) has the coordinates \(\left(0, \dfrac{b^2}{q}\right)\). Similarly, the \(y\)-coordinate of \(M\) is just the \(y\)-axis intercept of the line \(A^{\prime} P\), i.e. the line given by equation \(\eqref{eq:equation-Aprime-P}\), and hence \(M\) is given by \(\left(0, \dfrac{q a}{p + a}\right)\). Using this we get \[\begin{align*} OQ^2 - MQ^2 &= \left( \frac{b^2}{q} \right) ^2 - \left( \frac{b^2}{q} - \frac{q a}{p + a} \right)^2 \\ &= \left( \frac{b^2(p + a)}{q (p + a)} \right)^2 - \left( \frac{b^2(p + a) - q^2 a}{q (p + a)} \right)^2 \\ &= \frac{2q^2 a b^2 (p + a) - q^4 a^2}{q^2 (p + a)^2} \\ &= \frac{2a b^2 (p + a) - q^2 a^2}{(p + a)^2} \end{align*}\] Equation \(\eqref{eq:ellipse-eqn-eval-at-P}\) implies that \(q^2 = b^2 \left(1 - \dfrac{p^2}{a^2}\right)\) and using this for our calculation gives \[\begin{align*} OQ^2 - MQ^2 &= \frac{2a b^2 (p + a) - b^2 \left(1 - \frac{p^2}{a^2}\right) a^2}{(p + a)^2} \\ &= b^2 \frac{2a (p + a) - a^2 + p^2}{(p + a)^2} \\ &= b^2 \frac{2ap + 2a^2 - a^2 + p^2}{(p + a)^2} \\ &= b^2 \underbrace{\frac{p^2 + 2p a + a^2}{(p + a)^2}}_{= 1}. \end{align*}\]

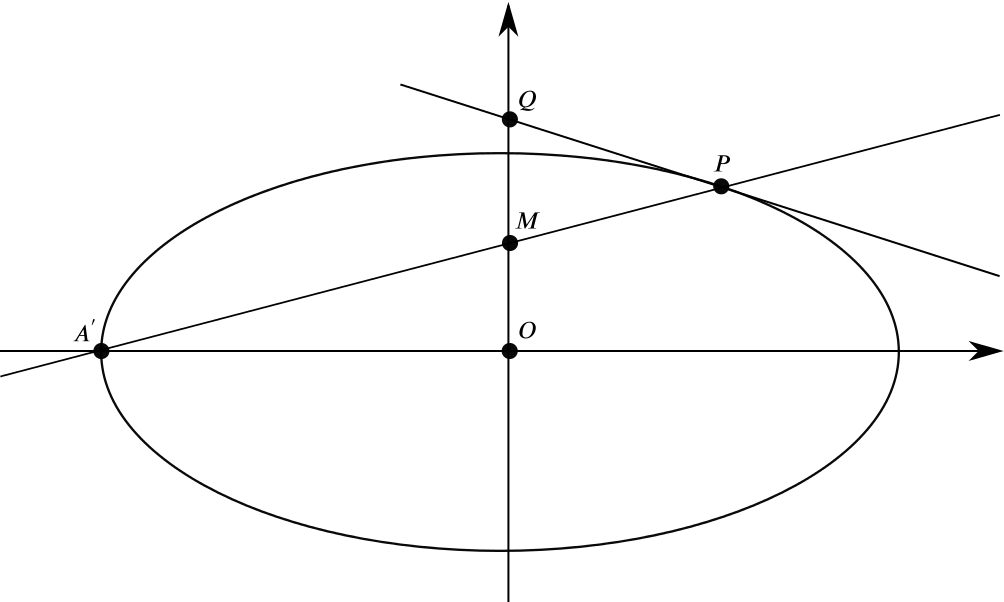
Thus \(OQ^2 - MQ^2 = b^2\).