When do these normals to a parabola meet on the parabola?

Add to your resource collection Remove from your resource collection Add notes to this resource View your notes for this resource

Taking the derivative of the equation \(y^2=4ax\) with respect to \(x\) we find that \[2y\frac{dy}{dx}=4a \qquad \Longrightarrow \qquad \frac{dy}{dx}=\frac{2a}{y}=\frac{2a}{2at}=\frac{1}{t}.\] The gradient of normal to the parabola at the point \((at^2,2at)\) is therefore \(-t\) since \[\frac{1}{t}\times -t=-1.\] The equation of the normal is then \[y-2at=-t(x-at^2) \qquad \Longrightarrow \qquad y=-tx+2at+at^3.\]

The gradient of the line \(PQ\) is \[\frac{2at_2-2at_1}{at_2^2-at_1^1}=\frac{2(t_2-t_1)}{(t_2-t_1)(t_1+t_2)}=\frac{2}{t_1+t_2}.\] The equation of the line through points \(P\) and \(Q\) is then \[y-2at_1=\frac{2}{t_1+t_2}(x-at_1^2).\] This will pass through the point \((-2a,0)\) if and only if \[\begin{align*} 0-2at_1&=\frac{2}{t_1+t_2}(-2a-at_1^2) \\ &\iff t_1 = \frac{1}{t_1+t_2}(2+t_1^2) \\ &\iff t_1(t_1+t_2) = 2+t_1^2 \\ &\iff t_1 t_2 = 2, \end{align*}\]

as required.

The two normals passing through \(P\) and \(Q\) have the equations \[\begin{align*} y &=-t_1x+2at_1+at_1^3 \\ y &=-t_2x+2at_2+at_2^3, \end{align*}\] using the first part of the question. They intersect when \[\begin{align*} -t_1x+2at_1+at_1^3 &= -t_2x+2at_2+at_2^3 \\ \Longrightarrow \qquad 2a(t_2-t_1)+a(t_2^3-t_1^3) &= x(t_2-t_1) \\ \end{align*}\] and factorising \((t_2^3-t_1^3)\) gives \[\begin{align*} \qquad 2a(t_2-t_1)+a(t_2-t_1)(t_1^2+t_1t_2+t_2^2) &= x(t_2-t_1) \end{align*}\] Since \(t_1\neq t_2\), as we are assuming \(P\) and \(Q\) are distinct, we can divide through by \((t_2-t_1)\) to get \[x=a(t_1^2+t_1t_2+t_2^2+2).\] Substituting for \(2=t_1t_2\) we find that \[\begin{align*} x &=a(t_1^2+2t_1t_2+t_2^2) \\ &= a(t_1+t_2)^2. \end{align*}\] Using this expression, we can substitute back into one of the original equations for the normal to find \[\begin{align*} y &= -t_1a(t_1+t_2)^2+2at_1+at_1^3 \\ &=-t_1^3a-2at_1^2t_2-at_1t_2^2+2at_1+at_1^3\\ &=-2a \times 2 \times t_1 - 2 \times at_2+2at_1\\ &= -2a(t_1+t_2). \end{align*}\]

Thus \(R=\left(a(t_1+t_2)^2,-2a(t_1+t_2)\right)\), and comparing this to the general point on the parabola \((at^2,2at)\), we can see that \(R\) is clearly on the curve.

Since \(P = (at_1^2, 2at_1)\), \(Q = (at_2^2, 2at_2)\), \(R = (a(t_1+t_2)^2, -2a(t_1+t_2))\), and \(O = (0, 0)\), then:

\(OP\) has gradient \(\dfrac{2}{t_1}\), \(PQ\) has gradient \(\dfrac{2}{t_1+t_2}\), \(QR\) has gradient \(-\dfrac{2}{t_1}\), while \(RO\) has gradient \(-\dfrac{2}{t_1+t_2}\).

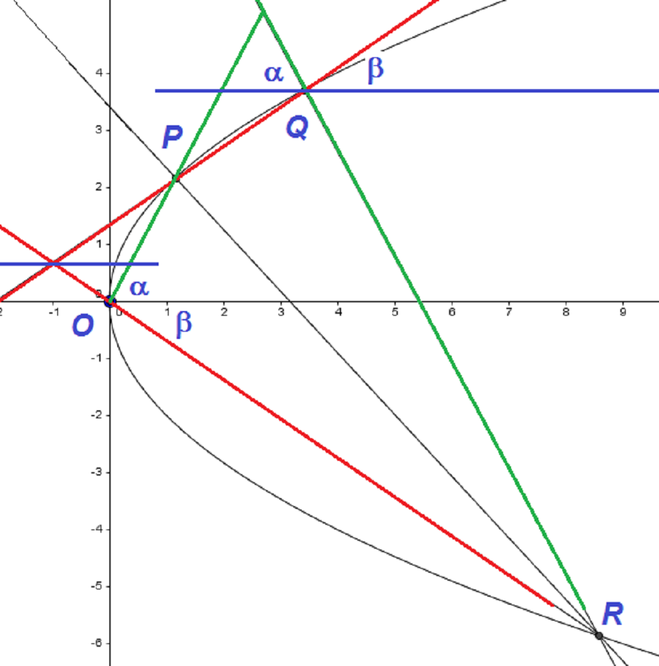
Thus \(OP\) and \(QR\) are reflections of each other in a vertical or horizontal line, and \(PQ\) and \(OR\) are likewise.

The diagram shows that angle \(\widehat{PQR}\) is \(180^\circ-\alpha -\beta\), and so the angles \(\widehat{POR}\) and \(\widehat{PQR}\) add to \(180^\circ\), and therefore \(OPQR\) is a cyclic quadrilateral.

Thus \(O\) lies on the circumcircle of \(PQR\), as required.