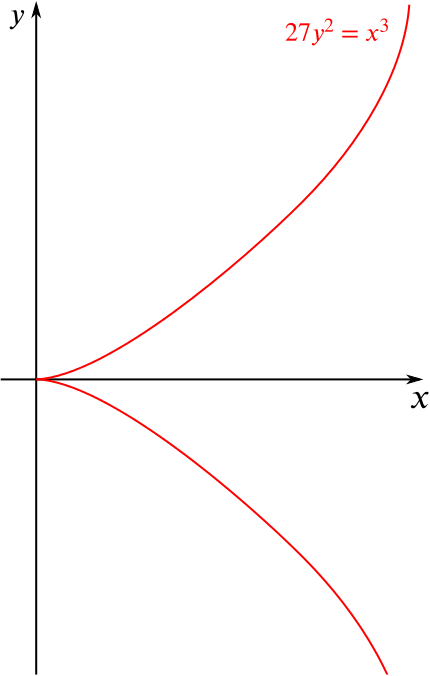
Sketch the form of the curve \(27y^2=x^3\), …
The graph passes through the point \((0,0)\), and at no other point crosses the \(x\)- or \(y\)-axis.
The graph does not exist for negative \(x\).
The curve will be symmetric about the \(x\)-axis, due to the \(y^2\) term.
We can rearrange the equation for positive \(y\) values as \(y=\frac{1}{\sqrt{27}}x^{3/2}\).
Since \(\dfrac{3}{2}>1\), this will be between the graph of \(y=x\) and \(y=x^2\), so it will look something like this…
… and find the equation of the tangent at the point \(P(12,8)\) on the curve.
Differentiating implicitly, we find that \[54y\frac{dy}{dx}=3x^2,\] and so \[\frac{dy}{dx}=\frac{1}{18}\frac{x^2}{y}.\] Evaluating this at \(P(12,8)\), the gradient of the tangent is \[\frac{1}{18}\frac{12^2}{8}=\frac{144}{144}=1.\] So the tangent has the form \[y=x+c.\]
Since we know that the tangent passes through \((12,8)\), we find that \[8=12+c \Longrightarrow c=-4.\] So the equation of the tangent to the curve at \(P\) is \[y=x-4.\]
Verify this tangent cuts the curve again at the point \(Q(3,-1)\).
For the line \(y=x-4\), we have \[-1=3-4=-1\] and so the line passes through \(Q\).
For the curve, we have \[27y^2=27\times (-1)^2=27\ \text{and}\ x^3=3^3=27.\]
So the curve and the line intersect again at \(Q(3,-1)\).
If \(O\) is the origin, find by integration the area enclosed by the arcs \(OP\), \(OQ\) of the curve and the line \(PQ\). [Integration with respect to \(y\) is recommended.]
Here’s the area we want to find:
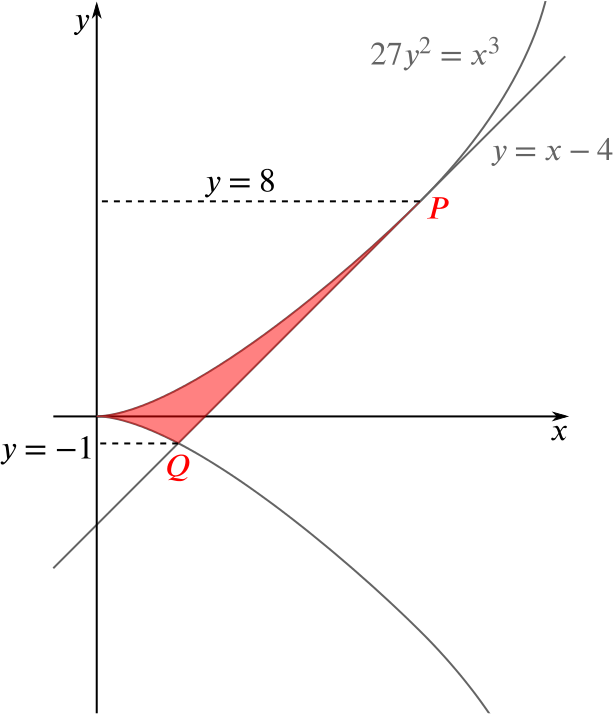
To find the shaded area, we find the area of the trapezium bounded by the lines \(x=0, y=8\), \(y=-1\) and \(PQ\) and then subtract the area under the curve \(x=3y^{2/3}\) between \(y=-1\) and \(y=8\).
The area of the trapezium is \[\frac{12+3}{2}\times 9=\frac{135}{2}.\]
The area under the curve is \[\begin{align*} \int_{-1}^8 3y^{2/3}\, dy &=\left[\frac{9}{5}y^{5/3}\right]^8_{-1}\\ &=\frac{9\times32}{5}+\frac{9}{5}\\ &=\frac{297}{5}. \end{align*}\]So the area we want is \[\frac{135}{2}-\frac{297}{5}=\frac{81}{10}.\]

