Show that the four points \((3,0)\), \((0,4)\), \((3,4)\), \((4,2)\) lie on a circle.
Find the centre and radius of this circle.
First method
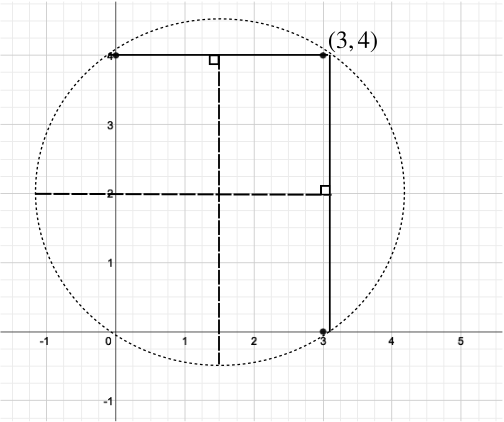
Let’s plot the points on a diagram:

Notice that the points \((3,0), (0,4)\) and \((3,4)\) form the vertices of a right-angled triangle. Therefore, when we draw a circle through these three points, it will have its diameter given by the hypotenuse of the triangle, and its centre at the midpoint of the hypotenuse.

The length of the hypotenuse is \(5\) by Pythagoras’ theorem, and the midpoint is at \(\left(\dfrac{3}{2},2\right)\). So the equation of the circle must be \[ \left(x-\dfrac{3}{2}\right)^2+(y-2)^2=\left(\dfrac{5}{2}\right)^2. \]
It remains to check that \((4,2)\) lies on this circle. The statement \[ \left(4-\dfrac{3}{2}\right)^2+(2-2)^2=\left(\dfrac{5}{2}\right)^2, \] is true, and so the four points \((3,0)\), \((0,4)\), \((3,4)\), \((4,2)\) lie on a circle, which has radius \(\dfrac{5}{2}\) and centre \(\left(\dfrac{3}{2},2\right)\).
Second method
A circle can always be drawn through any three points that do not lie on a straight line.
Take the general equation of a circle with centre \((a,b)\) and radius \(r\): \[(x-a)^2 + (y-b)^2 = r^2.\]
Now consider the first 3 points, \((3,0)\), \((0,4)\), \((3,4)\).
For the point \((3,0)\) to lie on this circle, we must have \[(3-a)^2 + b^2 = r^2.\]
Similarly, for the points \((0,4)\) and \((3,4)\) to lie on this circle, we must have \[a^2 + (4-b)^2 = r^2\] and \[(3-a)^2 + (4-b)^2 = r^2.\]
We will now solve these equations for \(a\), \(b\) and \(r\). Taking the first equation from the third gives \[(4-b)^2 - b^2 = 0\] which on expanding and solving (the \(b^2\) terms cancel) gives \(b = 2\).
Likewise, taking the second equation from the third gives \[(3-a)^2 - a^2 = 0\] so that \(a = \dfrac{3}{2}\).
Now substituting \(a = \dfrac{3}{2}\) and \(b = 2\) into the first equation gives \[\begin{align*} &\left(3-\frac{3}{2}\right)^2 + (2)^2 = r^2\\ \Longrightarrow\quad& r^2 = \frac{25}{4}\\ \Longrightarrow\quad& r = \frac{5}{2}. \end{align*}\]As a radius must be a positive length, we know that we must take the positive square root.
Therefore the circle has equation \[\left(x-\frac{3}{2}\right)^2 + (y-2)^2 = \frac{25}{4},\] so the circle has centre \(\left(\dfrac{3}{2}, 2\right)\) and radius \(\dfrac{5}{2}\).
Now we check the point \((4,2)\): the statement \[\left(4-\frac{3}{2}\right)^2 + (2-2)^2 = \frac{25}{4}.\] is true, so the point \((4,2)\) also lies on this circle.
Third method
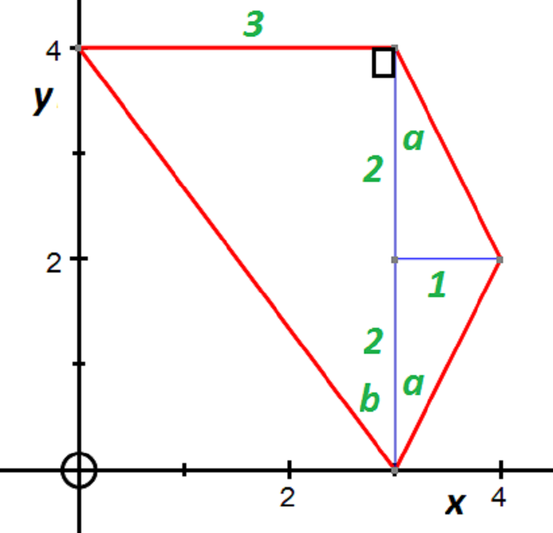
If we have two non-parallel chords in a circle, then their perpendicular bisectors intersect at the centre of the circle, as shown in the diagram.

So if we take the two chords joining the points \((3,0)\) and \((3,4)\), and \((3,4)\) and \((0,4)\) as shown below, then we know that the perpendicular bisectors of these chords must intersect at the centre of the circle passing through these three points.
As can be seen from the diagram, the perpendicular bisector of the line segment joining \((3,0)\) and \((3,4)\) is the line \[y = 2,\] and the perpendicular bisector of the line segment joining \((3,4)\) and \((0,4)\) is the line \[x = \frac{3}{2}.\]
So the centre of the circle passing through the points \((3,0)\), \((0,4)\) and \((3,4)\) is at \(\left(\dfrac{3}{2},2\right)\).
To find the radius, \(r\), of the circle, we need to find the distance from the centre, \(\left(\dfrac{3}{2},2\right)\), to any of the three points that we know lie on the circle, say \((3,0)\). We have
\[r = \sqrt{\left(\frac{3}{2}-3\right)^2 + (2-0)^2} = \sqrt{\frac{25}{4}} = \frac{5}{2}.\]
So we have the equation of the circle passing through the points \((3,0)\), \((0,4)\), \((3,4)\) as \[\left(x-\frac{3}{2}\right)^2 + (y-2)^2 = \frac{25}{4}.\]
It is easy to check that the point \((4,2)\) also lies on this circle.
Fourth method
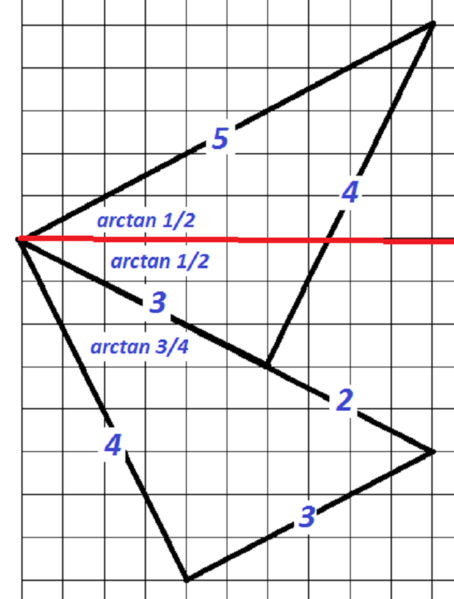
This method for showing the four points do indeed lie on a circle is included as a curiosity - the first three methods for doing the whole question are quicker!
If a circle can be drawn through four points, the quadrilateral they make is called cyclic.
Theorem; a quadrilateral is cyclic if and only if opposite angles add to \(180^o\). (Can you prove this?)
For this to be true here, we need \(2a + b = 90^0\).
In other words we need to show \(2\arctan(1/2) + \arctan(3/4) = 90^0\).