Show that the circles having equations \(x^2 + y^2 = 25\) and \(x^2 + y^2 - 24x - 18y + 125 = 0\) touch each other. Calculate the coordinates of the point at which they touch.
Approach 1: Geometric
The circle with equation \(x^2+y^2=25\) has its centre at the origin and radius \(5\).
We can complete the square for the equation \(x^2 + y^2 - 24x - 18y + 125 = 0\) to find its centre and radius: \[\begin{gathered} x^2 + y^2 - 24x - 18y + 125 = 0\\ \implies\quad (x-12)^2-12^2 + (y-9)^2 -9^2 + 125 = 0\\ \implies\quad (x-12)^2 + (y-9)^2 = 144+81-125\\ \implies\quad (x-12)^2 + (y-9)^2 = 100 \end{gathered}\] so this circle has centre \((12,9)\) and radius \(10\).
We can sketch these:
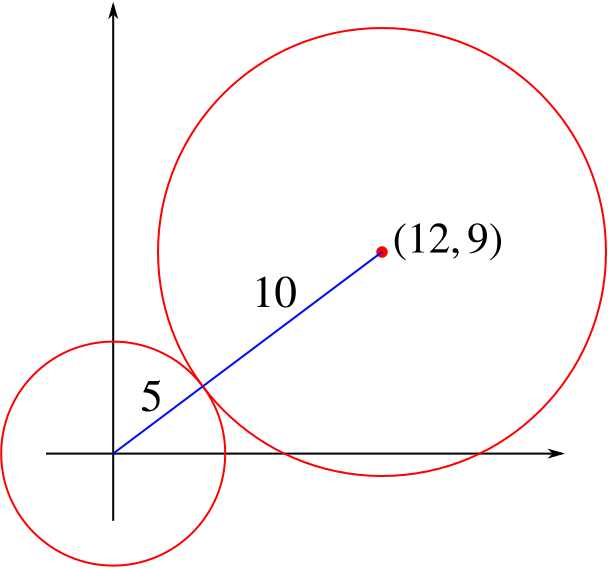
It seems as though the circles touch. Let’s prove that!
The length of the line joining the two centres \((0,0)\) and \((12,9)\) is (using Pythagoras) \[\sqrt{12^2+9^2}=\sqrt{144+81}=\sqrt{225}=15.\]
Alternatively, we can notice that \(9\) and \(12\) form the two short sides of right-angled triangle, which must be a \(3\)-\(4\)-\(5\) triangle scaled by a factor of \(3\), and therefore the diagonal length is \(3\times 5=15\).
Now the radii of the two circles are \(5\) and \(10\). Since \(5+10=15\) (the distance between the centres), the two circles touch.
To find the coordinates of the point where they touch, we can use similar triangles:
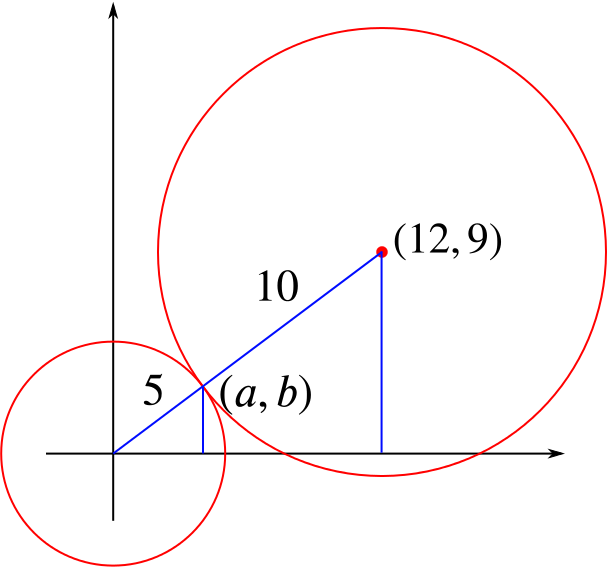
The small triangle has sides in the ratio \(a:b:5\) (base to height to hypotenuse), while in the large triangle, they are in the ratio \(12:9:15\). These ratios are the same, so \(a:b:5=4:3:5\), and the point of touching has coordinates \((4,3)\).
Another way to think about this is that the point of touching is \(\dfrac{5}{15}=\dfrac{1}{3}\) of the way along the line from \((0,0)\) to \((12,9)\), so it is at \((4,3)\).
Approach 2: Algebraic
For the circles to touch, we must show that they intersect at exactly one point.
We have the equations of the two circles: \[x^2 + y^2 = 25\] and \[x^2 + y^2 - 24x - 18y + 125 = 0.\]
Substituting the first equation into the second (or alternatively subtracting the first equation from the second) gives \[\begin{align*} &25 - 24x - 18y + 125 = 0\\ \Longrightarrow\quad& 24x + 18y = 150\\ \Longrightarrow\quad& 4x + 3y = 25. \end{align*}\]So if the two circles meet in two points, they must both lie on \(4x + 3y = 25.\)
The quadratic equation has a repeated root, so has exactly one solution.
This means that the line \(4x + 3y = 25\) is a tangent to the circle \(x^2 + y^2 = 25.\)
This means that the line \(4x + 3y = 25\) is a tangent to the second circle also at \((4,3)\).
So the circles \(x^2 + y^2 = 25\) and \(x^2 + y^2 - 24x - 18y + 125 = 0\) touch at the point \((4,3)\).

