\(ABCD\) is a square lying symmetrically inside a sector of a circle whose radius is \(\quantity{1}{in.}\), the angle of the sector being \(60^\circ\). \(A\) and \(B\) lie on the straight boundaries, \(C\) and \(D\) on the curved boundary. Calculate:
- the length of the arc \(CD\),
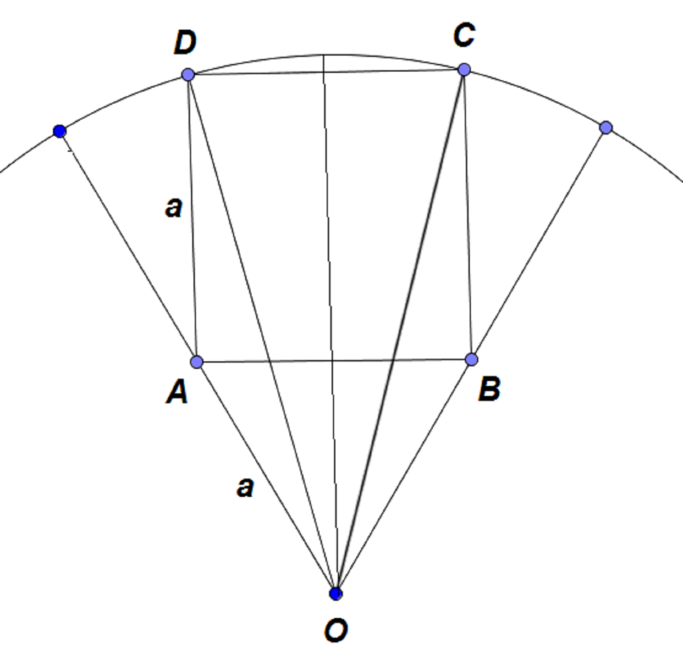
We have \(\angle OAB = \angle OBA\), and \(\angle AOB = 60^\circ\), so the triangle \(ABO\) is equilateral. Now consider the triangle \(ADO\). It is isosceles, with sides \(a, a\) and \(1\).
We have \(\angle OAD\) is \(150^\circ\), so we can say \(2a \sin 75 = 1\), and so \(a = \dfrac{1}{2 \sin 75} (\approx 0.5176...).\)
Now \(\angle DOA = 15^\circ = \angle COB\), since triangles \(DOA\) and \(COB\) are isosceles. Thus \(\angle DOC = 30^\circ\), and so \[\begin{align*} \text{length of the arc $CD$} &= \frac{\angle DOC}{360^\circ} \times \text{circumference of the circle} \\ &= \frac{30^\circ}{360^\circ} \times 2\pi \\ &= \quantity{\frac{\pi}{6}}{in.} \end{align*}\]- the area \(ABCD\),
This is simply \(a^2\), which is \(\left(\dfrac{1}{2 \sin 75}\right)^2 = \quantity{0.268(3sf)}{sq.in.}\)
We are not asked to find this exactly, but this is not hard to do. We have \(\sin 75 = \sin30\cos45+\sin45\cos30 = \dfrac{\sqrt{2}+\sqrt{6}}{4}.\)
So \(\left(\dfrac{1}{2 \sin 75}\right)^2 = \left(\dfrac{2}{\sqrt{2}+\sqrt{6}}\right)^2 = \dfrac{1}{2+\sqrt{3}} = 2-\sqrt{3} = \quantity{0.268(3sf)}{sq.in.}\)
- the area of the minor segment of the circle cut off by the chord \(CD\).
We need the area of the sector \(DOC\), and then subtract from this the area of the triangle \(DOC\).
Thus we have \(\pi \times 1^2 \times \dfrac{30}{360} - 0.5 \times 1 \times 1 \times \sin 30 = \quantity{\dfrac{\pi}{12} - \dfrac{1}{4}}{sq.in.}\)
Can you find any other ways of doing this question?

