Two coplanar circles, each of radius \(\quantity{5}{cm}\), have their centres \(\quantity{6}{cm}\) apart. Calculate the area of the region common to the interiors of both the circles, giving your answer in \(\mathrm{cm}^2\) correct to two significant figures.
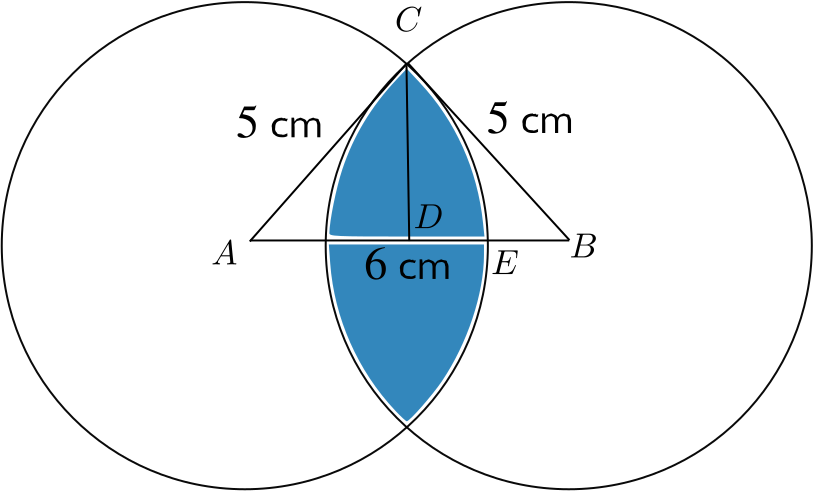
To calculate the shaded area, we’ll compute the area of the circle sector \(ACE\), before subtracting the area of the triangle \(ACD\), and then multiplying by \(4\).
The length \(AD\) must be \(3\), and so by Pythagoras, the length of \(CD\) must be \(4\). Thus \(\angle CAD\) is \(\arctan \dfrac{4}{3}\).
Thus the area of the sector \(ACE\) (working in radians) is \(0.5 \times 5^2 \times \arctan \dfrac{4}{3}\), while the area of triangle \(ACD\) is \(0.5 \times 4 \times 3 = 6\).
So the shaded area is \(4(12.5 \arctan \dfrac{4}{3}-6) = 22.36\dots\), which is \(\quantity{22}{cm^2}\) when given to two significant figures.

