Derive a condition for the two circles
\[\begin{align*} x^2+y^2+2g_1x+2f_1y+c_1 &= 0,\\ x^2+y^2+2g_2x+2f_2y+c_2 &= 0, \end{align*}\]to cut orthogonally.
If we complete the square for each equation (by adding \(+g^2 - g^2 +f^2 -f^2\) to the left hand side), we find
\[\begin{align} \label{eq:1} (x+g_1)^2+(y+f_1)^2 &= g_1^2 +f_1^2 -c_1,\\ \nonumber (x+g_2)^2+(y+f_2)^2 &= g_2^2 +f_2^2 -c_2. \end{align}\]The centres are \((-g_1,-f_1)\) and \((-g_2,-f_2)\), and
\[\begin{align} \label{eq:2} r_1^2 = g_1^2 +f_1^2 -c_1,\\ \nonumber r_2^2 = g_2^2 +f_2^2 -c_2. \end{align}\]If two circles cut orthogonally, their radii and the line connecting their centres form a right triangle.
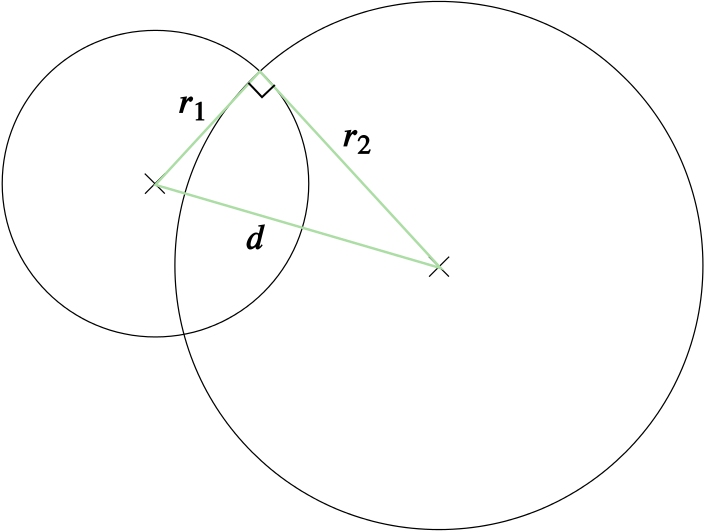
Hence, using Pythagoras, we have
\[\begin{equation} \label{eq:3} r_1^2 + r_2^2 = d^2=(g_1-g_2)^2+(f_1-f_2)^2. \end{equation}\]Now we have
\[\begin{align*} g_1^2 +f_1^2 -c_1 + g_2^2 +f_2^2 -c_2 &= (g_1-g_2)^2+(f_1-f_2)^2\\ \implies c_1 + c_2 &= 2g_1g_2 + 2f_1f_2.\\ \end{align*}\]This is the condition for the given circles to cut orthogonally.
Hence, or otherwise, show that in general there is just one circle orthogonal to three given circles.
Given three circles, let’s define them via
\[\begin{align*} x^2+y^2+2g_1x+2f_1y+c_1 &= 0,\\ x^2+y^2+2g_2x+2f_2y+c_2 &= 0,\\ x^2+y^2+2g_3x+2f_3y+c_3 &= 0. \end{align*}\]Can the unknown circle \(x^2+y^2+2Gx+2Fy+C = 0\) be orthogonal to all three circles? If so, we have three equations for three unknowns:
\[\begin{align*} I:&& C + c_1 &= 2Gg_1 + 2Ff_1,\\ II:&& C + c_2 &= 2Gg_2 + 2Ff_2,\\ III:&& C + c_3 &= 2Gg_3 + 2Ff_3. \end{align*}\]In general, three equations for three unknowns can be solved to give a unique solution.
There are special cases when, for example, two of the circles coincide, where the solution will not be unique, or when the three equations have no solutions (imagine three circles of equal radius with their centres collinear that don’t intersect) but we’ve been asked about the general case.
Find the centre and radius of the circle orthogonal to the three circles
\[\begin{align*} x^2+y^2-12x-8y+34 &= 0,\\ x^2+y^2-6x-12y+32 &= 0,\\ x^2+y^2-10x-6y+30 &= 0. \end{align*}\]We need to solve simultaneously the three equations
\[\begin{align*} I:&& C + 34 &= 2G(-6) + 2F(-4),\\ II:&& C + 32 &= 2G(-3) + 2F(-6),\\ III:&& C + 30 &= 2G(-5) + 2F(-3). \end{align*}\]Subtracting the second from the first, and the third from the first, we derive the two equations in \(G\) and \(F\) \[2=-6G+4F, 4=-2G+-2F.\]
Adding twice the second to the first here gives \(10=-10G\), and so \(G = -1, F = -1, C = -14\).
Thus the circle orthogonal to all three circles is \((x+1)^2 + (y+1)^2 =16\), which has centre \((-1, -1)\), and radius \(4\).

