Two equal circles, each of radius \(\quantity{10}{cm}\), have centres at \(A\) and \(B\) respectively and the length of \(AB\) is \(\quantity{17.4}{cm}\). The circles intersect at \(C\) and \(D\). Find
- the angle \(CBA\) and express it in radians correct to three significant figures,
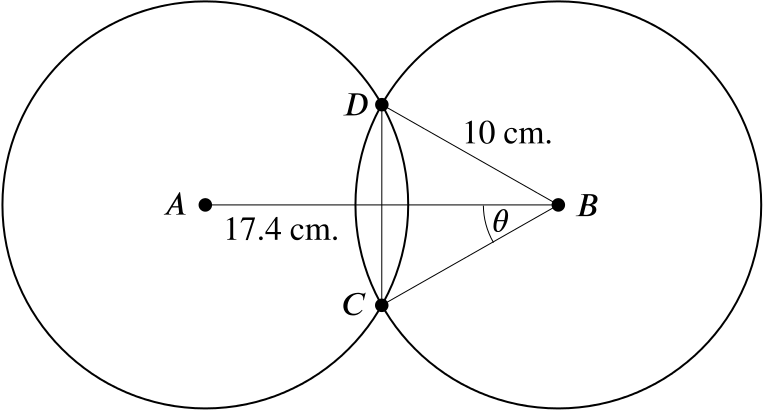
The line segment \(CD\) is the perpendicular bisector of \(AB\), and so we have the following right-angled triangle.
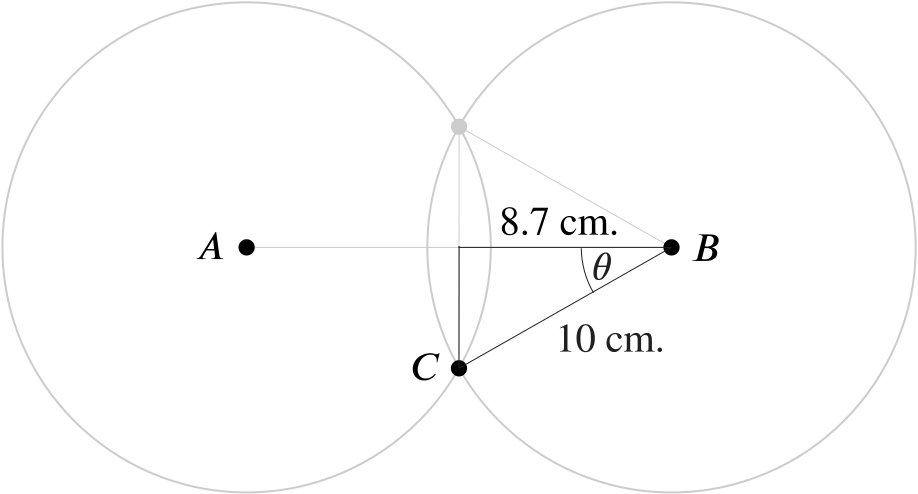
Thus, \[ \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\quantity{8.7}{cm}}{\quantity{10}{cm}} = 0.87 \] and so \[ \theta = \arccos(0.87) = \text{$0.51559\!\ldots$ radians} \] which, to three significant figures, is \(0.516\) radians.
- the area of the minor sector \(BCD\),
By symmetry, \(\theta = \angle CBA = \angle DBA\), and so \[ \angle DBC = \angle DBA + \angle CBA = 2\theta = 2 \arccos(0.87). \]
The area of a sector of radius \(r\) and enclosed angle \(\theta\) (in radians) is \(\dfrac{1}{2}r^2\theta\), so the area of the sector \(CDB\) is \(\dfrac{1}{2}10^2(2 \arccos(0.87)) = 51.559...,\)
which to \(3\)sf is \(\quantity{51.6}{cm^2}.\)
- the area common to both circles.
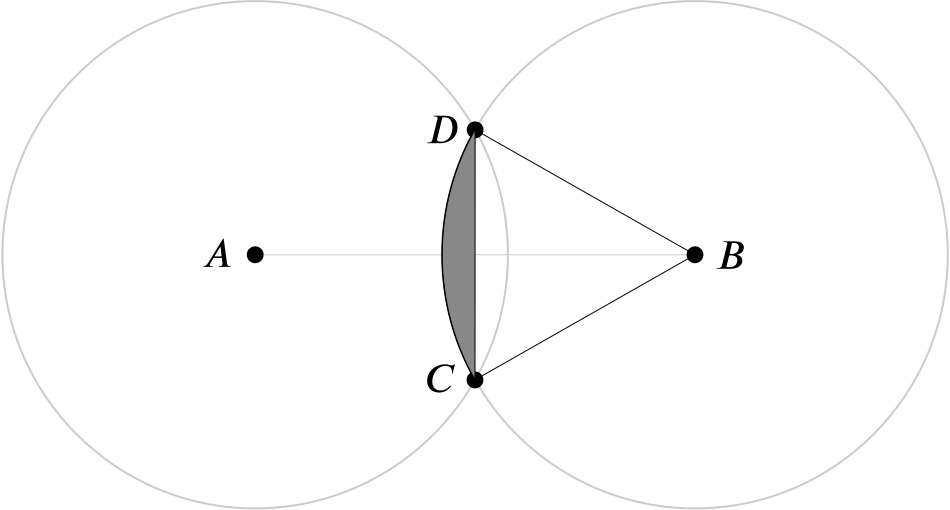
By symmetry, the area common to both circles is twice the area of this shaded region, and the area of this shaded region is equal to \[ \text{area of the minor sector $BCD$} - \text{area of $\triangle BCD$}. \]
The area of a triangle is \(\dfrac{1}{2}ab \sin C\), so the triangle \(BCD\) has area \(\dfrac{1}{2}100 \sin (2\arccos(0.87))=42.895...\)
Thus the area of the shaded region is \(51.559... - 42.895... = 8.664...,\) and so the area shared between the circles is (\(3\)sf) \(\quantity{17.3}{cm^2}.\)

