Two circles of radius \(\quantity{3}{in.}\) touch each other, and a third circle of radius \(\quantity{2}{in.}\) touches each of them externally. Find the area contained between the three circles.

The part of the diagram shaded in red is the area we need to find. We’ll find the area of the triangle, and subtract the areas of the sectors of the three circles.
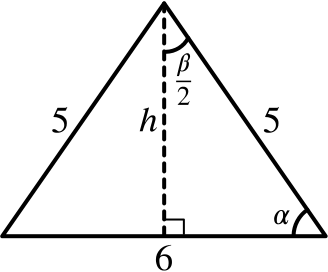
We need to find the height of the triangle and the angle \(\alpha\). We can see that (working in radians) \(\beta= \pi - 2 \alpha\).
Using Pythagoras’ theorem, we see that \[ h=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4. \] So the area of the triangle is \[ \frac{1}{2}\times 6\times 4=\quantity{12}{in.^2} \] By trigonometry, it is clear that \[ \cos\alpha=\frac{3}{5}, \quad \sin\alpha=\frac{4}{5}. \]
Let’s compute the areas of the sectors. The area of a sector (working in radians) of radius \(r\) and enclosing an angle \(\theta\) is \(\dfrac{1}{2}r^2\theta\).
Thus the sectors with radius three each have area \[ \frac{1}{2}\times 3^2 \times \alpha =\frac{9}{2}\arccos(0.6), \] and the sector with radius \(2\) has area \[ \frac{1}{2}\times 2^2 \times (\pi-2\arccos(0.6)) = 2\pi - 4\arccos(0.6). \] Thus the red area is \[\begin{align*} \text{area of triangle}-2\times \text{area of big sector}- \text{area of small sector} \\ =\quantity{12-5\arccos(0.6)-2\pi}{in.^2} \approx \quantity{1.08}{in.^2} \end{align*}\]
